11.7 SUDOKU¶
SUDOKU is a famous simple yet mind-blowing game. The objective is to fill a 9×9 grid with digits so that each column, each row, and each of the nine 3×3 sub-grids that compose the grid (also called boxes, blocks, regions, or sub-squares) contains all of the digits from 1 to 9. For more information see http://en.wikipedia.org/wiki/Sudoku. Here is a simple example:
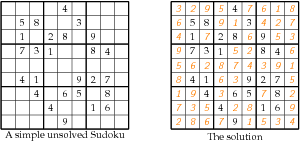
In a more general setting we are given a grid of dimension \(n\times n\), with \(n=m^2, m\in \natnumb\). Each cell \((i,j)\) must be filled with an integer \(y_{ij} \in [1,n]\). Along each row and each column there must be no repetitions. No repetitions are allowed also in each sub-grid with corners \(\{(mt,ml),\ (m(t+1)-1,m(l+1)-1)\}\), for \(t,l=0,\ldots,m-1\) (we index cells from \((0,0)\)).
In general, each SUDOKU instance comes with a set \(F\) of predetermined values which:
reduce the complexity of the game by removing symmetries and guiding the initial moves of the player;
ensure that there will be a unique solution.
We represent the set \(F\) as list of triplets \((i,j,v)\), meaning that the cell \((i,j)\) contains the value \(v\).
Note that SUDOKU is a feasibility problem. A typical Integer Programming formulation is straightforward: let \(x_{ijk}\) be a binary variable that takes value \(1\) if \(k\) is written in cell \((i,j)\). Then we look for a feasible solution of a system of constraints given below.
SUDOKU is a typical assignment problem. Its constraints are commonly found in optimization problems concerning scheduling or resource allocation. SUDOKU has also been a nice problem to fiddle with for many researchers in the optimization community. Indeed, its simple structure and the easy way in which the results can be tested make it a perfect test problem.
We will approach SUDOKU as a standard integer linear program, and we will show how easily and elegantly it can be implemented in Fusion.
Mathematical Formulation
In this section we formulate SUDOKU as a mixed-integer linear optimization problem. Let’s introduce a binary variable \(x_{ijk}\) that takes value \(1\) if \(k\) is written in the cell \((i,j)\), or \(0\) otherwise. We first ask that for each cell exactly one digit is selected:
Similar constraints can be used to force each digit to appear only once in each row or column:
To force a digit to appear only once in each sub-grid we can use the following
If a cell \((i,j)\) has a predetermined value, i.e. \((i,j,k)\in F\) then we set
Summarizing, and considering that there is no objective function to minimize, the optimization model for the SUDOKU problem takes the form
Implementation with Fusion
The implementation in Fusion is straightforward. First, we represent the variable \(x\) using a three dimensional Fusion variable:
x = M.variable("x",[n, n, n], Domain.binary())
Then we can define constraints (11.27) and (11.28) simply using the Expr.sum operator, that allows to sum the elements of an expression (in this case of the variable itself) along arbitrary dimensions. The code reads:
#each value only once per dimension
for d in range(m):
M.constraint("row_sum(%d)" % d, Expr.sum(x, d) == 1)
The last set of constraints (11.29) , i.e. the sum over block, needs a little more effort: we must loop over all blocks and select the proper slice:
#each number must appear only once in a block
for k in range(n):
for i in range(m):
for j in range(m):
M.constraint("blocksum(%d,%d,k=%d)" % (i,j,k),
Expr.sum(x[i*m : (i+1)*m, j*m : (j+1)*m, k : (k+1)]) == 1)
To set the triplets given in the set \(F\) we can use the Variable.pick ([]) method that returns a one dimensional view of an arbitrary set of elements of the variable.
M.constraint("fix", x.pick(fixed) == 1.0)
SUDOKU: the complete example code.
The complete code for the SUDOKU problem is shown in Listing 11.16.
import sys
import mosek
from mosek.fusion import *
import mosek.fusion.pythonic
import numpy as npy
def print_solution(m, x):
n = m * m
print("\n")
for i in range(n):
ss = ""
for j in range(n):
if j % m == 0:
ss = ss + " |"
for k in range(n):
if x.index([i, j, k]).level() > 0.5:
ss = ss + " " + str(k + 1)
break
print(ss + ' |')
if (i + 1) % m == 0:
print("\n")
def main():
m = 3
n = m * m
hr_fixed = [[1, 5, 4],
[2, 2, 5], [2, 3, 8], [2, 6, 3],
[3, 2, 1], [3, 4, 2], [3, 5, 8], [3, 7, 9],
[4, 2, 7], [4, 3, 3], [4, 4, 1], [4, 7, 8], [4, 8, 4],
[6, 2, 4], [6, 3, 1], [6, 6, 9], [6, 7, 2], [6, 8, 7],
[7, 3, 4], [7, 5, 6], [7, 6, 5], [7, 8, 8],
[8, 4, 4], [8, 7, 1], [8, 8, 6],
[9, 5, 9]
]
fixed = [[f[0] - 1, f[1] - 1, f[2] - 1] for f in hr_fixed]
with Model('SUDOKU') as M:
x = M.variable("x",[n, n, n], Domain.binary())
#each value only once per dimension
for d in range(m):
M.constraint("row_sum(%d)" % d, Expr.sum(x, d) == 1)
#each number must appear only once in a block
for k in range(n):
for i in range(m):
for j in range(m):
M.constraint("blocksum(%d,%d,k=%d)" % (i,j,k),
Expr.sum(x[i*m : (i+1)*m, j*m : (j+1)*m, k : (k+1)]) == 1)
M.constraint("fix", x.pick(fixed) == 1.0)
M.setLogHandler(sys.stdout)
M.solve()
M.writeTask("sudoku.task")
#print the solution, if any...
if M.getPrimalSolutionStatus() in [SolutionStatus.Optimal]:
print_solution(m, x)
else:
print("No solution found!")
if __name__ == '__main__':
main()
The problem instance corresponding to Fig. 11.8 is hard-coded for the sake of simplicity. It will produce the following output
Problem
Name : SUDOKU
Objective sense : min
Type : LO (linear optimization problem)
Constraints : 350
Cones : 0
Scalar variables : 1000
Matrix variables : 0
Integer variables : 729
Optimizer started.
Mixed integer optimizer started.
Threads used: 2
Presolve started.
Presolve terminated. Time = 0.00
Presolved problem: 0 variables, 0 constraints, 0 non-zeros
Presolved problem: 0 general integer, 0 binary, 0 continuous
Clique table size: 0
BRANCHES RELAXS ACT_NDS DEPTH BEST_INT_OBJ BEST_RELAX_OBJ REL_GAP(%) TIME
0 1 0 0 0.0000000000e+00 0.0000000000e+00 0.00e+00 0.0
An optimal solution satisfying the relative gap tolerance of 1.00e-02(%) has been located.
The relative gap is 0.00e+00(%).
An optimal solution satisfying the absolute gap tolerance of 0.00e+00 has been located.
The absolute gap is 0.00e+00.
Objective of best integer solution : 0.000000000000e+00
Best objective bound : -0.000000000000e+00
Construct solution objective : Not employed
Construct solution # roundings : 0
User objective cut value : 0
Number of cuts generated : 0
Number of branches : 0
Number of relaxations solved : 1
Number of interior point iterations: 0
Number of simplex iterations : 0
Time spend presolving the root : 0.00
Time spend in the heuristic : 0.00
Time spend in the sub optimizers : 0.00
Time spend optimizing the root : 0.00
Mixed integer optimizer terminated. Time: 0.02
Optimizer terminated. Time: 0.02
| 3 2 9 | 5 4 7 | 6 1 8 |
| 6 5 8 | 9 1 3 | 4 2 7 |
| 4 1 7 | 2 8 6 | 9 5 3 |
| 9 7 3 | 1 5 2 | 8 4 6 |
| 5 6 2 | 8 7 4 | 3 9 1 |
| 8 4 1 | 6 3 9 | 2 7 5 |
| 1 9 4 | 3 6 5 | 7 8 2 |
| 7 3 5 | 4 2 8 | 1 6 9 |
| 2 8 6 | 7 9 1 | 5 3 4 |
