13.4 The Optimizer for Mixed-Integer Problems¶
Solving optimization problems where one or more of the variables are constrained to be integer valued is called Mixed-Integer Optimization (MIO). For an introduction to model building with integer variables, the reader is recommended to consult the MOSEK Modeling Cookbook, and for further reading we highlight textbooks such as [Wol98] or [CCornuejolsZ14].
MOSEK can perform mixed-integer linear (MILO) and conic (MICO) problems, except for mixed-integer semidefinite problems.
By default the mixed-integer optimizer is run-to-run deterministic. This means that if a problem is solved twice on the same computer with identical parameter settings and no time limit, then the obtained solutions will be identical. The mixed-integer optimizer is parallelized, i.e., it can exploit multiple cores during the optimization.
In practice, it often happens that the integer variables in MIO problems are actuall binary variables, taking values in \(\{0,1\}\), leading to Mixed- or pure binary problems. In the general setting however, an integer variable may have arbitrary lower and upper bounds.
13.4.1 Branch-and-Bound¶
In order to succeed in solving mixed-integer problems, it can be useful to have a basic understanding of the underlying solution algorithms. The most important concept in this regard is arguably the so-called Branch-and-Bound algorithm, employed also by MOSEK. The more experienced reader may skip this section and advance directly to Sec. 13.4.2 (Solution quality and termination criteria).
In order to comprehend Branch-and-Bound, the concept of a relaxation is important. Consider for example a mixed-integer linear optimization problem of minimization type
It has the continuous relaxation
simply obtained by ignoring the integrality restrictions. The first step in Branch-and-Bound is to solve this so-called root relaxation, which is a continuous optimization problem. Since (13.13) is less constrained than (13.12), one certainly gets
and \(\underline{z}\) is therefore called the objective bound: it bounds the optimal objective value from below.
After the solution of the root relaxation, in the most likely outcome there will be one or more integer constrained variables with fractional values, i.e., violating the integrality constraints. Branch-and-Bound now takes such a variable, \(x_j = f_j\in\mathbb{R}\setminus\mathbb{Z}\) with \(j\in\mathcal{J}\), say, and creates two branches leading to relaxations with the additional constraint \(x_j \leq \lfloor f_j \rfloor\) or \(x_j \geq \lceil f_j \rceil\), respectively. The intuitive idea here is to exclude the undesired fractional value from the outcomes in the two created branches. If the integer variable was actually a binary variable, branching would lead to fixing its value to \(0\) in one branch, and to \(1\) in the other.
The Branch-and-Bound process continues in this way and successively solves relaxations and creates branches to refined relaxations. Whenever the solution \(\hat{x}\) to some relaxation does not violate any integrality constraints, it is feasible to (13.12) and is called an integer feasible solution. There is no guarantee though that it is also optimal, its solution value \(\bar{z} := c^T \hat{x}\) is only an upper bound on the optimal objective value,
By the successive addition of constraints in the created branches, the objective bound \(\underline{z}\) (now defined as the minimum over all solution values of so far solved relaxations) can only increase during the algorithm. At the same time, the upper bound \(\bar{z}\) (the solution value of the best integer feasible solution encountered so far, also called incumbent solution) can only decrease during the algorithm. Since at any time we also have
objective bound and incumbent solution value are encapsulating the optimal objective value, eventually converging to it.
The Branch-and-Bound scheme can be depicted by means of a tree, where branches and relaxations correspond to edges and nodes. Figure Fig. 13.1 shows an example of such a tree. The strength of Branch-and-Bound is its ability to prune nodes in this tree, meaning that no new child nodes will be created. Pruning can occur in several cases:
A relaxation leads to an integer feasible solution \(\hat{x}\). In this case we may update the incumbent and its solution value \(\bar{z}\), but no new branches need to be created.
A relaxation is infeasible. The subtree rooted at this node cannot contain any feasible relaxation, so it can be discarded.
A relaxation has a solution value that exceeds \(\bar{z}\). The subtree rooted at this node cannot contain any integer feasible solution with a solution value better than the incumbent we already have, so it can be discarded.
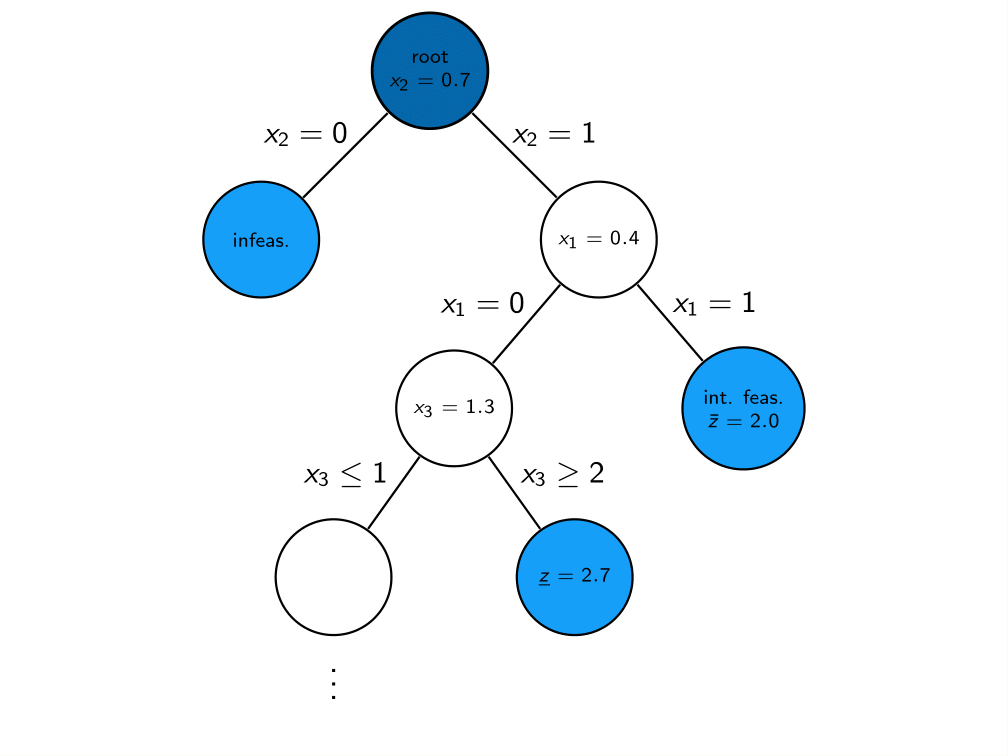
Fig. 13.1 An examplary Branch-and-Bound tree. Pruned nodes are shown in light blue.¶
Having objective bound and incumbent solution value is a quite fundamental property of Branch-and-Bound, and helps to asses solution quality and control termination of the algorithm, as we detail in the next section. Note that the above explanation is coined for minimization problems, but the Branch-and-bound scheme has a straightforward extension to maximization problems.
13.4.2 Solution quality and termination criteria¶
The issue of terminating the mixed-integer optimizer is rather delicate. Mixed-integer optimization is generally much harder than continuous optimization; in fact, solving continuous sub-problems is just one component of a mixed-integer optimizer. Despite the ability to prune nodes in the tree, the computational effort required to solve mixed-integer problems grows exponentially with the size of the problem in a worst-case scenario (solving mixed-integer problems is NP-hard). For instance, a problem with \(n\) binary variables, may require the solution of \(2^n\) relaxations. The value of \(2^n\) is huge even for moderate values of \(n\). In practice it is often advisable to accept near-optimal or appproximate solutions in order to counteract this complexity burden. The user has numerous possibilities of influencing optimizer termination with various parameters, in particular related to solution quality, and the most important ones are highlighted here.
13.4.2.1 Solution quality in terms of optimality¶
In order to assess the quality of any incumbent solution in terms of its objective value, one may check the optimality gap, defined as
\[\epsilon= |\mbox{(incumbent solution value)}-\mbox{(objective bound)}| = |\bar{z}-\underline{z}|.\]
It measures how much the objectives of the incumbent and the optimal solution can deviate in the worst case. Often it is more meaningful to look at the relative optimality gap
\[\epsilon_{\textrm{rel}} = \frac{|\bar{z}-\underline{z}|}{\max(\delta_1, |\bar{z}|)}.\]
This is essentially the above absolute optimality gap normalized against the magnitude of the incumbent solution value; the purpose of the (small) constant \(\delta_1\) is to avoid overweighing incumbent solution values that are very close to zero. The relative optimality gap can thus be interpreted as answering the question: “Within what fraction of the optimal solution is the incumbent solution in the worst case?”
Absolute and relative optimality gaps provide useful means to define termination criteria for the mixed-integer optimizer in MOSEK. The idea is to terminate the optimization process as soon as the quality of the incumbent solution, measured in absolute or relative gap, is good enough. In fact, whenever an incumbent solution is located, the criterion
is checked. If satisfied, i.e., if either absolute or relative optimality gap are below the thresholds \(\delta_2\) or \(\delta_3\) (see Table 13.3), the optimizer terminates and reports the incumbent as an optimal solution. The optimality gaps at termination can always be retrieved through the information items "mioObjAbsGap" and "mioObjRelGap".
The tolerances discussed above can be adjusted using suitable parameters, see Table 13.3. By default, the optimality parameters \(\delta_2\) and \(\delta_3\) are quite small, i.e., restrictive. These default values for the absolute and relative gap amount to solving any instance to (almost) optimality: the incumbent is required to be within at most a tiny percentage of the optimal solution. As anticipated, this is not tractable in many practical situations, and one should resort to finding near-optimal solutions quickly rather than insisting on finding the optimal one. It may happen, for example, that an optimal or close-to-optimal solution is found very early by the optimizer, but it spends a huge amount of further computational time for branching, trying to increase \(\underline{z}\) that last missing bit: a typical situation that practioneers would want to avoid. The concept of optimality gaps is fundamental for controlling solution quality when resorting to near-optimal solutions.
MIO performance tweaks: termination criteria
One of the first things to do in order to cut down excessive solution time is to increase the relative gap tolerance mioTolRelGap to some non-default value, so as to not insist on finding optimal solutions. Typical values could be \(0.01, 0.05\) or \(0.1\), guaranteeing that the delivered solutions lie within \(1\%, 5\%\) or \(10\%\) of the optimum. Increasing the tolerance will lead to less computational time spent by the optimizer.
13.4.2.2 Solution quality in terms of feasibility¶
For an optimizer relying on floating-point arithmetic like the mixed-integer optimizer in MOSEK, it may be hard to achieve exact integrality of the solution values of integer variables in most cases, and it makes sense to numerically relax this constraint. Any candidate solution \(\hat{x}\) is accepted as integer feasible if the criterion
is satisfied, meaning that \(\hat{x_j}\) is at most \(\delta_4\) away from the nearest integer. As above, \(\delta_4\) can be adjusted using a parameter, see Table 13.3, and impacts the quality of the acieved solution in terms of integer feasibility. By influencing what solution may be accepted as imcumbent, it can also have an impact on the termination of the optimizer.
MIO performance tweaks: feasibility criteria
Whether increasing the integer feasibility tolerance mioTolAbsRelaxInt leads to less solution time is highly problem dependent. Intuitively, the optimizer is more flexible in finding new incumbent soutions so as to improve \(\bar{z}\). But this effect has do be examined with care on indivuidual instances: it may worsen solution quality with no effect at all on the solution time. It may in some cases even lead to contrary effects on the solution time.
Tolerance |
Parameter name |
Default value |
|---|---|---|
\(\delta_1\) |
1.0e-10 |
|
\(\delta_2\) |
0.0 |
|
\(\delta_3\) |
1.0e-4 |
|
\(\delta_4\) |
1.0e-5 |
13.4.2.3 Further controlling optimizer termination¶
There are more ways to limit the computational effort employed by the mixed-integer optimizer by simply limiting the number of explored branches, solved relaxations or updates of the incumbent solution. When any of the imposed limits is hit, the optimizer terminates and the incumbent solution may be retrieved. See Table 13.4 for a list of corresponding parameters. In contrast to the parameters discussed in Sec. 13.4.2.1 (Solution quality in terms of optimality), interfering with these does not maintain any guarantees in terms of solution quality.
Parameter name |
Explanation |
|---|---|
Maximum number of branches allowed. |
|
Maximum number of relaxations allowed. |
|
Maximum number of feasible integer solutions allowed. |
13.4.3 The Mixed-Integer Log¶
The Branch-and-Bound scheme from Sec. 13.4.1 (Branch-and-Bound) is only the basic skeleton of the mixed-integer optimizer in MOSEK, and several components are built on top of that in order to enhance its functionality and increase its speed. A mixed-integer optimizer is sometimes referred to as a “giant bag of tricks”, and it would be impossible to describe all of these tricks here. Yet, some of the additional components are worth mentioning. They can be influenced by various user parameters, and although the default values of these parameters are optimized to work well on average mixed-integer problems, it may pay off to adjust them for an individual problem, or a specific problem class. The mixed-integer log can give insights on which parameters might be worth an adjustment. Below is a typical log output:
Presolve started.
Presolve terminated. Time = 0.23, probing time = 0.09
Presolved problem: 1176 variables, 1344 constraints, 4968 non-zeros
Presolved problem: 328 general integer, 392 binary, 456 continuous
Clique table size: 55
Symmetry factor : 0.79 (detection time = 0.01)
Removed blocks : 2
BRANCHES RELAXS ACT_NDS DEPTH BEST_INT_OBJ BEST_RELAX_OBJ REL_GAP(%) TIME
0 0 1 0 8.3888091139e+07 NA NA 0.2
0 1 1 0 8.3888091139e+07 2.5492512136e+07 69.61 0.3
0 1 1 0 3.1273162420e+07 2.5492512136e+07 18.48 0.4
0 1 1 0 2.6047699632e+07 2.5492512136e+07 2.13 0.4
Rooot cut generation started.
0 1 1 0 2.6047699632e+07 2.5492512136e+07 2.13 0.4
0 2 1 0 2.6047699632e+07 2.5589986247e+07 1.76 0.4
Rooot cut generation terminated. Time = 0.05
0 4 1 0 2.5990071367e+07 2.5662741991e+07 1.26 0.5
0 8 1 0 2.5971002767e+07 2.5662741991e+07 1.19 0.6
0 11 1 0 2.5925040617e+07 2.5662741991e+07 1.01 0.6
0 12 1 0 2.5915504014e+07 2.5662741991e+07 0.98 0.6
2 23 1 0 2.5915504014e+07 2.5662741991e+07 0.98 0.7
14 35 1 0 2.5915504014e+07 2.5662741991e+07 0.98 0.7
[ ... ]
Objective of best integer solution : 2.578282162804e+07
Best objective bound : 2.569877601306e+07
Construct solution objective : Not employed
User objective cut value : Not employed
Number of cuts generated : 192
Number of Gomory cuts : 52
Number of CMIR cuts : 137
Number of clique cuts : 3
Number of branches : 29252
Number of relaxations solved : 31280
Number of interior point iterations: 16
Number of simplex iterations : 105440
Time spend presolving the root : 0.23
Time spend optimizing the root : 0.07
Mixed integer optimizer terminated. Time: 6.96
The main part here is the iteration log, a progressing series of similar rows reflecting the progress made during the Branch-and-bound process. The columns have the following meanings:
BRANCHES: Number of branches / nodes generated.RELAXS: Number of relaxations solved.ACT_NDS: Number of active / non-processed nodes.DEPTH: Depth of the last solved node.BEST_INT_OBJ: The incumbent solution / best integer objective value, \(\bar{z}\).BEST_RELAX_OBJ: The objective bound, \(\underline{z}\).REL_GAP(%): Relative optimality gap, \(100\%\cdot\epsilon_{\textrm{rel}}\)TIME: Time (in seconds) from the start of optimization.
Also a short solution summary with several statistics is printed. When the solution time for a mixed-integer problem has to be cut down, the log can help to understand where time is spent and what might be improved. We go into some more detail about some further items in the mixed-integer log giving hints about individual components of the optimizer. Alternatively, most of these items can also be retrieved as information items, see Sec. 8.5 (Retrieving information items).
13.4.3.1 Presolve¶
Similar to the case of continuous problems, see Sec. 13.1 (Presolve), the mixed-integer optimizer applies various presolve reductions before the actual Branch-and-bound is initiated. The first lines of the mixed-integer log contain a summary of the presolve process, including the time spent therein (Presolve terminated. Time = 0.23...). Just as in the continuous case, the use of presolve can be controlled with the parameter presolveUse. If presolve time seems excessive, instead of switching it off completely one may also try to reduce the time spent in one or more of its individual components. On some models it can also make sense to increase the use of a certain presolve technique. Table Table 13.5 lists some of these with their respective parameters.
Parameter name |
Explanation |
Possible reference in log |
|---|---|---|
Probing aggressivity level. |
|
|
Symmetry detection aggressivity level. |
|
|
Block structure detection level, see Sec. 13.4.3.5 (Block decomposition). |
|
|
Maximum size of the clqiue table. |
|
|
Should variable agggregation be enabled? |
– |
13.4.3.2 Primal Heuristics¶
It might happen that the value in the colum BEST_INT_OBJ stalls over a long period of log lines, an indication that the optimizer has a hard time improving the incumbent solution, i.e., \(\bar{z}\). Solving relaxations in the tree to an integer feasible solution \(\hat{x}\) is not the only way to find new incumbent solutions. There is a variety of procedures that, given a mixed-integer problem in a generic form like (13.12), attempt to produce integer feasible solutions in an ad-hoc way. These procedures are called Primal Heuristics, and several of them are implemented in MOSEK. For example, whenever a relaxation leads to a fractional solution, one may round the solution values of the integer variables, in various ways, and hope that the outcome is still feasible to the remaining constraints. Primal heuristics are mostly employed while processing the root node, but play a role throughout the whole solution process. The goal of a primal heuristic is to improve the incumbent solution and thus the bound \(\bar{z}\), and this can of course affect the quality of the solution that is returned after termination of the optimizer. The user parameters affecting primal heuristics are listed in Table 13.6.
MIO performance tweaks: primal heuristics
If the mixed-integer optimizer struggles to improve the incumbent solution
BEST_INT_OBJ, it can be helpful to intensify the use of primal heuristics.Set parameters related to primal heuristics to more aggressive values than the default ones, so that more effort is spent in this component. A List of the respective parameters can be found in Table 13.6. In particular, if the optimizer has difficulties finding any integer feasible solution at all, indicated by
NAin the columnBEST_INT_OBJin the mixed-integer log, one may try to activate a construction heuristic like the Feasibility Pump withmioFeaspumpLevel.Specify a good initial solution: In many cases a good feasible solution is either known or easily computed using problem-specific knowledge that the optimizer does not have. If so, it is usually worthwhile to use this as a starting point for the mixed-integer optimizer. See also the parameter
mioConstructSol, and Section Sec. 7.7.2 (Specifying an initial solution).For feasibility problems, i.e., problems having a constant objective, the goal is to find a single integer feasible solution, and this can be hard by itself on some instances. Try setting the objective to something meaningful anyway, even if the underlying application does not require this. After all, the feasible set is not changed, but the optimizer might benefit from being able to pursue a concrete goal.
In rare cases it may also happen that the optimizer spends an excessive amount of time on primal heuristics without drawing any benefit from it, and one may try to limit their use with the respective parameters.
Parameter name |
Explanation |
|---|---|
Primal heuristics aggressivity level. |
|
Maximum number of nodes allowed in the RINS heuristic. |
|
Maximum number of nodes allowed in the RENS heuristic. |
|
Maximum number of nodes allowed in the Crossover heuristic. |
|
Maximum number of nodes allowed in the optimal face heuristic. |
|
Way of using the Feasibility Pump heuristic. |
13.4.3.3 Cutting Planes¶
It might as well happen that the value in the colum BEST_RELAX_OBJ stalls over a long period of log lines, an indication that the optimizer has a struggles to improve the objective bound \(\underline{z}\). A component of the optimizer designed to act on the objective bound is given by Cutting planes, also called cuts or valid inequalities. Cuts do not remove any integer feasible solutions from the feasible set of the mixed-integer problem (13.12). They may, however, remove solutions from the feasible set of the relaxation (13.13), ideally making it a stronger relaxation with better objective bound.
As an example, take the constraints
One may realize that there cannot be a feasible solution in which both binary variables take on a value of \(1\). So certainly
is a valid inequality (there is no integer solution satisfying (13.14), but violating (13.15)). The latter does cut off a portion of the feasible region of the continuous relaxation of (13.14) though, obtained by replacing \(x_1,x_2\in\{0,1\}\) with \(x_1,x_2\in[0,1]\). For example, the fractional point \((x_1, x_2, x_3) = (0.5, 1, 0)\) is feasible to the relaxation, but violates the cut (13.15).
There are many classes of general-purpose cuttting planes that may be generated for a mixed-integer problem in a generic form like (13.12), and MOSEK’s mixed-integer optimizer supports several of them. For instance, the above is an example of a so-called clique cut. The most effort on generating cutting planes is spent after the solution of the root relaxation; the beginning and the end of root cut generation is highlighted in the log, and the number of log lines in between reflects to the computational effort spent here. Also the solution summary at the end of the log highlights for each cut class the number of generated cuts. Cuts can also be generated later on in the tree, which is why we also use the term Branch-and-cut, an extension of the basic Branch-and-bound scheme. Cuts aim at improving the objective bound \(\underline{z}\) and can thus have significant impact on the solution time. The user parameters affecting cut generation can be seen in Table 13.7.
MIO performance tweaks: cutting planes
If the mixed-integer optimizer struggles to improve the objective bound
BEST_RELAX_OBJ, it can be helpful to intensify the use of cutting planes.Some types of cutting planes are not activated by default, but doing so may help to improve the objective bound.
The parameters
mioTolRelDualBoundImprovementandmioCutSelectionLeveldetermine how aggressively cuts will be generated and selected.If some valid inequalities can be deduced from problem-specific knowledge that the optimizer does not have, it may be helpful to add these to the problem formulation as constraints. This has to be done with care, since there is a tradeoff between the benefit obtained from an improved objective boud, and the amount of additional constraints that make the relaxations larger.
In rare cases it may also be observed that the optimizer spends an excessive effort on cutting planes, and one may limit their use with
mioMaxNumRootCutRounds, or by disabling a certain type of cutting planes.
Parameter name |
Explanation |
|---|---|
Should clique cuts be enabled? |
|
Should mixed-integer rounding cuts be enabled? |
|
Should GMI cuts be enabled? |
|
Should implied bound cuts be enabled? |
|
Should knapsack cover cuts be enabled? |
|
Should lift-and-project cuts be enabled? |
|
Cut selection aggressivity level. |
|
Maximum number of root cut rounds. |
|
Minimum required objective bound improvement during root cut generation. |
13.4.3.4 Restarts¶
The mixed-integer optimizer employs so-called restarts, i.e., if the progress made while exploring the tree is deemed unsufficient, it might decide to restart the solution process from scratch, possibly making use of the information collected so far. When a restart happens, this is displayed in the log:
[ ... ]
1948 4664 699 36 NA 1.1800000000e+02 NA 7.2
1970 4693 705 50 NA 1.1800000000e+02 NA 7.2
Performed MIP restart 1.
Presolve started.
Presolve terminated. Time = 0.01, probing time = 0.00
Presolved problem: 523 variables, 765 constraints, 3390 non-zeros
Presolved problem: 0 general integer, 404 binary, 119 continuous
Clique table size: 143
BRANCHES RELAXS ACT_NDS DEPTH BEST_INT_OBJ BEST_RELAX_OBJ REL_GAP(%) TIME
1988 4729 1 0 NA 1.1800000000e+02 NA 7.3
1988 4730 1 0 4.0000000000e+01 1.1800000000e+02 195.00 7.3
[ ... ]
Restarts tend to be useful especially for hard models. However, in individual cases the optimizer may decide to perform a restart while it would have been better to continue exploring the tree. Their use can be controlled with the parameter mioMaxNumRestarts.
13.4.3.5 Block decomposition¶
Sometimes the optimizer faces a model that actually represents two or more completely independent subproblems. For a linear problem such as (13.13), this means that the constraint matrix \(A\) is a block-diagonal. Block-diagonal structure can occur after MOSEK applies some presolve reductions, e.g., a variable is fixed that was the only variable connecting two otherwise independent subproblems. Or, more rarely, the original model provided by the user is already block-diagonal.
In principle, solving such blocks independently is easier than letting the optimizer work on the single, large model, and MOSEK thus tries to exploit this structure. Some blocks may be completely solved and removed from the model during presolve, which can be seen by a line at the end of the presolve summary, see also Sec. 13.4.3.1 (Presolve). If after presolve there are still independent blocks, MOSEK can apply a dedicated algorithm to solve them independently while periodically combining their individual solution statusses (such as incumbent solutions and objective bounds) to the solution status of the original model. Just like the removal of blocks during presolve, the application of this latter strategy is indicated in the log:
[ ... ]
15 38 1 0 4.1759800000e+05 3.8354200000e+05 8.16 0.9
Root cut generation started.
15 38 1 0 4.1759800000e+05 3.8354200000e+05 8.16 1.1
Root cut generation terminated. Time = 0.11
15 40 1 0 4.1645600000e+05 3.8934425000e+05 6.51 2.0
15 41 1 0 4.1622400000e+05 3.8934425000e+05 6.46 2.0
23 52 1 0 4.1622400000e+05 3.8934425000e+05 6.46 2.0
Decomposition solver started with 5 independent blocks.
532 425 5 118 4.1592600000e+05 3.8935275000e+05 6.39 4.5
1858 11911 815 286 4.1007800000e+05 3.8946400000e+05 5.03 11.8
[ ... ]
How block-diagonal structure is detected and handled by the optimizer can be controlled with the parameter mioIndependentBlockLevel.
13.4.4 Mixed-Integer Nonlinear Optimization¶
Due to the involved non-linearities, MI(QC)QO or MICO problems are on average harder than MILO problems of comparable size. Yet, the Branch-and-Bound scheme can be applied to these probelm classes in a straightforward manner. The relaxations have to be solved as conic problems with the interior point algorithm in that case, see Sec. 13.3 (Conic Optimization - Interior-point optimizer), opposed to MILO where it is often beneficial to solve relaxations with the dual simplex method, see Sec. 13.2.3 (The Simplex Optimizer). There is another solution approach for these types of problems implemented in MOSEK, namely the Outer-Approximation algorithm, making use of dynamically refined linear approximations of the non-linearities.
MICO performance tweaks: choice of algorithm
Whether conic Branch-and-Bound or Outer-Approximation is applied to a mixed-integer conic problem can be set with mioConicOuterApproximation. The best value for this option is highly problem dependent.
13.4.5 Disjunctive constraints¶
Problems with disjunctive constraints (DJC) see Sec. 7.8 (Disjunctive constraints) are typically reformulated to mixed-integer problems, and even if this is not the case they are solved with an algorithm that is based on the mixed-integer optimizer. In MOSEK, these problems thus fall into the realm of MIO. In particular, MOSEK automatically attempts to replace any DJC by so called big-M constraints, potentially after transforming it to several, less complicated DJCs. As an example, take the DJC
where \(z\in\{0,1\}\) and \(x_1, x_2 \in [0,750]\). This is an example of a DJC formulation of a so-called indicator constraint. A big-M reformulation is given by
where \(M > 0\) is a large constant. The practical difficulty of these constructs is that \(M\) should always be sufficiently large, but ideally not larger. Too large values for \(M\) can be harmful for the mixed-integer optimizer. During presolve, and taking into account the bounds of the involved variables, MOSEK automatically reformulates DJCs to big-M constraints if the required \(M\) values do not exceed the parameter mioDjcMaxBigm. From a performance point-of-view, all DJCs would ideally be linearized to big-Ms after presolve without changing this parameter’s default value of 1.0e6. Whether or not this is the case can be seen by retrieving the information item "mioPresolvedNumdjc", or by a line in the mixed-integer optimizer’s log as in the example below. Both state the number of remaining disjunctions after presolve.
Presolved problem: 305 variables, 204 constraints, 708 non-zeros
Presolved problem: 0 general integer, 100 binary, 205 continuous
Presolved problem: 100 disjunctions
Clique table size: 0
BRANCHES RELAXS ACT_NDS DEPTH BEST_INT_OBJ BEST_RELAX_OBJ REL_GAP(%) TIME
0 1 1 0 NA 0.0000000000e+00 NA 0.0
0 1 1 0 5.0574653969e+05 0.0000000000e+00 100.00 0.0
[ ... ]
DJC performance tweaks: managing variable bounds
Always specify the tightest known bounds on the variables of any problem with DJCs, even if they seem trivial from the user-perspective. The mixed-integer optimizer can only benefit from these when reformulating DJCs and thus gain performance; even if bounds don’t help with reformulations, it is very unlikely that they hurt the optimizer.
Increasing
mioDjcMaxBigmcan lead to more DJC reformulations and thus increase optimizer speed, but it may in turn hurt numerical solution quality and has to be examined with care. The other way round, on numerically challenging instances with DJCs, decreasingmioDjcMaxBigmmay lead to numerically more robust solutions.
13.4.6 Randomization¶
A mixed-integer optimizer is usually prone to performance variability, meaning that a small change in either
problem data, or
computer hardware, or
algorithmic parameters
can lead to significant changes in solution time, due to different solution paths in the Branch-and-cut tree. In extreme cases the exact same problem can vary from being solvable in less than a second to seemingly unsolvable in any reasonable amount of time on a different computer.
One practical implication of this is that one should ideally verify whether a seemingly beneficial set of parameters, established experimentally on a single problem, is still beneficial (on average) on a larger set of problems from the same problem class. This protects against making parameter changes that had positive effects only due to random effects on that single problem.
In the absence of a large set of test problems, one may also change the random seed of the optimizer to a series of different values in order to hedge against drawing such wrong conclusions regarding parameters. The random seed, accessible through mioSeed, impacts for example random tie-breaking in many of the mixed-integer optimizer’s components. Changing the random seed can be combined with a permutation of the problem data to further incite randomness, accessible through the parameter mioDataPermutationMethod.
13.4.7 Further performance tweaks¶
In addition to what was mentioned previously, there may be other ways to speed up the solution of a given mixed-integer problem. For example, there are further user parameters affecting some algorithmic settings in the mixed-integer optimizer. As mentioned above, default parameter values are optimized to work well on average, but on individual problems they may be adjusted.
MIO performance tweaks: miscellaneous
While exploring the tree, the optimizer applies certain strategies to decide which fractional variable to branch on, see Sec. 13.4.1 (Branch-and-Bound). The chosen strategy can have a big impact on performance, and may be controlled with
mioVarSelection.Similarly, the strategy to chose the next node to explore in the tree is controlled with
mioNodeSelection.The optimizer employs specialized techniques to learn from infeasible nodes and use that knowledge to avoid creating similar nodes in other parts of the tree. The effort spent here can be influenced with
mioDualRayAnalysisLevelandmioConflictAnalysisLevel.When relaxations in the tree are linear optimization problems (e.g., in MILO or when solving MICO probelms with the Outer-Approximation method), it is usually best to employ the dual simplex method for their solution. In rare cases the primal simplex method may actually be the better choice, and this can be set with the parameter
mioNodeOptimizer.Some problems are numerically more challenging than others, for example if the ratio between the smallest and the largest involved coefficients is large, say \(\geq 1e9\). An indication of numerical issues are, for example, large violations in the final solution, observable in the solution summery of the log output, see Sec. 9.1.3 (Mixed-integer problem). Similarly, a problem that is known to be feasible by the user may be declared infeasible by the optimizer. In such cases it is usually best to try to rescale the model. Otherwise, the mixed-integer optimizer can be instructed to be more cautios regarding numerics with the parameter
mioNumericalEmphasisLevel. This may in turn be at the cost of solution speed though.Improve the formulation: A MIO problem may be impossible to solve in one form and quite easy in another form. However, it is beyond the scope of this manual to discuss good formulations for mixed-integer problems. For discussions on this topic see for example [Wol98].
