10.3 Logistic regression

Logistic regression is an example of a binary classifier, where the output takes one two values 0 or 1 for each data point. We call the two values classes.

Formulation as an optimization problem

Define the sigmoid function

\[S(x)=\frac{1}{1+\exp(-x)}.\]

Next, given an observation \(x\in\real^d\) and a weights \(\theta\in\real^d\) we set

\[h_\theta(x)=S(\theta^Tx)=\frac{1}{1+\exp(-\theta^Tx)}.\]

The weights vector \(\theta\) is part of the setup of the classifier. The expression \(h_\theta(x)\) is interpreted as the probability that \(x\) belongs to class 1. When asked to classify \(x\) the returned answer is

\[\begin{split}x\mapsto \begin{cases}\begin{array}{ll}1 & h_\theta(x)\geq 1/2, \\ 0 & h_\theta(x)<1/2.\end{array}\end{cases}\end{split}\]

When training a logistic regression algorithm we are given a sequence of training examples \(x_i\), each labelled with its class \(y_i\in \{0,1\}\) and we seek to find the weights \(\theta\) which maximize the likelihood function

\[\prod_i h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{1-y_i}.\]

Of course every single \(y_i\) equals 0 or 1, so just one factor appears in the product for each training data point. By taking logarithms we can define the logistic loss function:

\[J(\theta) = -\sum_{i:y_i=1} \log(h_\theta(x_i))-\sum_{i:y_i=0}\log(1-h_\theta(x_i)).\]

The training problem with regularization (a standard technique to prevent overfitting) is now equivalent to

\[\min_\theta J(\theta) + \lambda\|\theta\|_2.\]

This can equivalently be phrased as

(10.21)\[\begin{split}\begin{array}{lrllr} \minimize & \sum_i t_i +\lambda r & & & \\ \st & t_i & \geq - \log(h_\theta(x)) & = \log(1+\exp(-\theta^Tx_i)) & \mathrm{if}\ y_i=1, \\ & t_i & \geq - \log(1-h_\theta(x)) & = \log(1+\exp(\theta^Tx_i)) & \mathrm{if}\ y_i=0, \\ & r & \geq \|\theta\|_2. & & \end{array}\end{split}\]

Implementation

As can be seen from (10.21) the key point is to implement the softplus bound \(t\geq \log(1+e^u)\), which is the simplest example of a log-sum-exp constraint for two terms. Here \(t\) is a scalar variable and \(u\) will be the affine expression of the form \(\pm \theta^Tx_i\). This is equivalent to

\[\exp(u-t) + \exp(-t)\leq 1\]

and further to

(10.22)\[\begin{split}\begin{array}{rclr} (z_1, 1, u-t) & \in & \EXP & (z_1\geq \exp(u-t)), \\ (z_2, 1, -t) & \in & \EXP & (z_2\geq \exp(-t)), \\ z_1+z_2 & \leq & 1. & \end{array}\end{split}\]

This formulation can be entered using affine conic constraints (see Sec. 6.2 (From Linear to Conic Optimization)).

Listing 10.13 Implementation of (10.21). Click here to download.

logisticRegression <- function(X, y, lamb)
{
    prob <- list(sense="min")
    n <- dim(X)[1];
    d <- dim(X)[2];
    
    # Variables: r, theta(d), t(n), z1(n), z2(n)
    prob$c <- c(lamb, rep(0,d), rep(1, n), rep(0,n), rep(0,n));
    prob$bx <-rbind(rep(-Inf,1+d+3*n), rep(Inf,1+d+3*n));

    # z1 + z2 <= 1
    prob$A <- sparseMatrix( rep(1:n, 2), 
                            c((1:n)+1+d+n, (1:n)+1+d+2*n),
                            x = rep(1, 2*n));
    prob$bc <- rbind(rep(-Inf, n), rep(1, n));

    # (r, theta) \in \Q
    FQ <- cbind(diag(rep(1, d+1)), matrix(0, d+1, 3*n));
    gQ <- rep(0, 1+d);

    # (z1(i), 1, -t(i)) \in \EXP, 
    # (z2(i), 1, (1-2y(i))*X(i,) - t(i)) \in \EXP
    FE <- Matrix(nrow=0, ncol = 1+d+3*n);
    for(i in 1:n) {
        FE <- rbind(FE,
                    sparseMatrix( c(1, 3, 4, rep(6, d), 6),
                                  c(1+d+n+i, 1+d+i, 1+d+2*n+i, 2:(d+1), 1+d+i),
                                  x = c(1, -1, 1, (1-2*y[i])*X[i,], -1),
                                  dims = c(6, 1+d+3*n) ) );
    }
    gE <- rep(c(0, 1, 0, 0, 1, 0), n);

    prob$F <- rbind(FQ, FE)
    prob$g <- c(gQ, gE)
    prob$cones <- cbind(matrix(list("QUAD", 1+d, NULL), nrow=3, ncol=1),
                        matrix(list("PEXP", 3, NULL), nrow=3, ncol=2*n));
    rownames(prob$cones) <- c("type","dim","conepar")

    # Solve, no error handling!
    r <- mosek(prob, list(soldetail=1))

    # Return theta
    r$sol$itr$xx[2:(d+1)]
}

Example: 2D dataset fitting

In the next figure we apply logistic regression to the training set of 2D points taken from the example ex2data2.txt . The two-dimensional dataset was converted into a feature vector \(x\in\real^{28}\) using monomial coordinates of degrees at most 6.

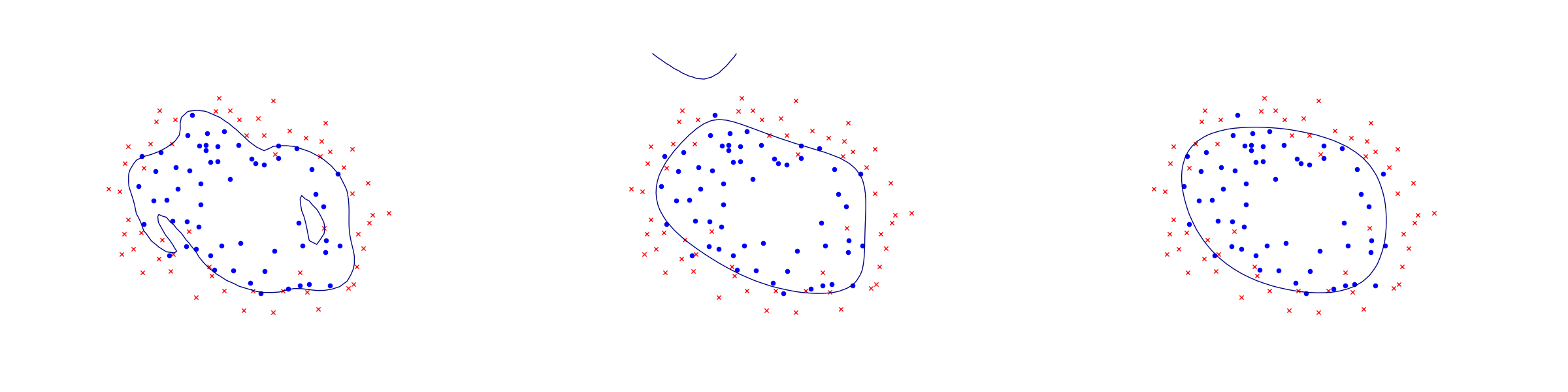
Fig. 10.4 Logistic regression example with none, medium and strong regularization (small, medium, large \(\lambda\)). Without regularization we get obvious overfitting.