11.2 Logistic regression

Logistic regression is an example of a binary classifier, where the output takes one two values 0 or 1 for each data point. We call the two values classes.

Formulation as an optimization problem

Define the sigmoid function

\[S(x)=\frac{1}{1+\exp(-x)}.\]

Next, given an observation \(x\in\real^d\) and a weights \(\theta\in\real^d\) we set

\[h_\theta(x)=S(\theta^Tx)=\frac{1}{1+\exp(-\theta^Tx)}.\]

The weights vector \(\theta\) is part of the setup of the classifier. The expression \(h_\theta(x)\) is interpreted as the probability that \(x\) belongs to class 1. When asked to classify \(x\) the returned answer is

\[\begin{split}x\mapsto \begin{cases}\begin{array}{ll}1 & h_\theta(x)\geq 1/2, \\ 0 & h_\theta(x)<1/2.\end{array}\end{cases}\end{split}\]

When training a logistic regression algorithm we are given a sequence of training examples \(x_i\), each labelled with its class \(y_i\in \{0,1\}\) and we seek to find the weights \(\theta\) which maximize the likelihood function

\[\prod_i h_\theta(x_i)^{y_i}(1-h_\theta(x_i))^{1-y_i}.\]

Of course every single \(y_i\) equals 0 or 1, so just one factor appears in the product for each training data point. By taking logarithms we can define the logistic loss function:

\[J(\theta) = -\sum_{i:y_i=1} \log(h_\theta(x_i))-\sum_{i:y_i=0}\log(1-h_\theta(x_i)).\]

The training problem with regularization (a standard technique to prevent overfitting) is now equivalent to

\[\min_\theta J(\theta) + \lambda\|\theta\|_2.\]

This can equivalently be phrased as

(11.13)\[\begin{split}\begin{array}{lrllr} \minimize & \sum_i t_i +\lambda r & & & \\ \st & t_i & \geq - \log(h_\theta(x)) & = \log(1+\exp(-\theta^Tx_i)) & \mathrm{if}\ y_i=1, \\ & t_i & \geq - \log(1-h_\theta(x)) & = \log(1+\exp(\theta^Tx_i)) & \mathrm{if}\ y_i=0, \\ & r & \geq \|\theta\|_2. & & \end{array}\end{split}\]

Implementation

As can be seen from (11.13) the key point is to implement the softplus bound \(t\geq \log(1+e^u)\), which is the simplest example of a log-sum-exp constraint for two terms. Here \(t\) is a scalar variable and \(u\) will be the affine expression of the form \(\pm \theta^Tx_i\). This is equivalent to

\[\exp(u-t) + \exp(-t)\leq 1\]

and further to

(11.14)\[\begin{split}\begin{array}{rclr} (z_1, 1, u-t) & \in & \EXP & (z_1\geq \exp(u-t)), \\ (z_2, 1, -t) & \in & \EXP & (z_2\geq \exp(-t)), \\ z_1+z_2 & \leq & 1. & \end{array}\end{split}\]

This formulation can be entered using affine conic constraints (see Sec. 6.2 (From Linear to Conic Optimization)).

Listing 11.8 Implementation of \(t\geq \log(1+e^u)\) as in (11.14). Click here to download.

    // Adds ACCs for t_i >= log ( 1 + exp((1-2*y[i]) * theta' * X[i]) )
    // Adds auxiliary variables, AFE rows and constraints
    public static void softplus(Task task, int d, int n, int theta, int t, double[,] X, bool[] y)
    {
      int nvar = task.getnumvar();
      int ncon = task.getnumcon();
      long nafe = task.getnumafe();
      task.appendvars(2*n);   // z1, z2
      task.appendcons(n);     // z1 + z2 = 1
      task.appendafes(4*n);   //theta * X[i] - t[i], -t[i], z1[i], z2[i]
      int z1 = nvar, z2 = nvar+n;
      int zcon = ncon;
      long thetaafe = nafe, tafe = nafe+n, z1afe = nafe+2*n, z2afe = nafe+3*n;
      int k = 0;

      // Linear constraints
      int[]    subi = new int[2*n];
      int[]    subj = new int[2*n];
      double[] aval = new double[2*n];

      for(int i = 0; i < n; i++)
      {
        // z1 + z2 = 1
        subi[k] = zcon+i;  subj[k] = z1+i;  aval[k] = 1;  k++;
        subi[k] = zcon+i;  subj[k] = z2+i;  aval[k] = 1;  k++;
      }
      task.putaijlist(subi, subj, aval);
      task.putconboundsliceconst(zcon, zcon+n, boundkey.fx, 1, 1);
      task.putvarboundsliceconst(nvar, nvar+2*n, boundkey.fr, -inf, inf);

      // Affine conic expressions
      long[]   afeidx = new long[d*n+4*n];
      int[]    varidx = new int[d*n+4*n];
      double[] fval   = new double[d*n+4*n];
      k = 0;

      // Thetas
      for(int i = 0; i < n; i++) {
        for(int j = 0; j < d; j++) {
          afeidx[k] = thetaafe + i; varidx[k] = theta + j; 
          fval[k] = ((y[i]) ? -1 : 1) * X[i,j];
          k++;
        }
      }

      // -t[i]
      for(int i = 0; i < n; i++) {
        afeidx[k] = thetaafe + i; varidx[k] = t + i; fval[k] = -1; k++;
        afeidx[k] = tafe + i;     varidx[k] = t + i; fval[k] = -1; k++;
      }

      // z1, z2
      for(int i = 0; i < n; i++) {
        afeidx[k] = z1afe + i; varidx[k] = z1 + i; fval[k] = 1; k++;
        afeidx[k] = z2afe + i; varidx[k] = z2 + i; fval[k] = 1; k++;
      }

      // Add the expressions
      task.putafefentrylist(afeidx, varidx, fval);

      // Add a single row with the constant expression "1.0"
      long oneafe = task.getnumafe();
      task.appendafes(1);
      task.putafeg(oneafe, 1.0);

      // Add an exponential cone domain
      long expdomain = task.appendprimalexpconedomain();
      
      // Conic constraints
      for(int i = 0; i < n; i++)
      {
        task.appendacc(expdomain, new long[]{z1afe+i, oneafe, thetaafe+i}, null);
        task.appendacc(expdomain, new long[]{z2afe+i, oneafe, tafe+i}, null);
      }
    }

Once we have this subroutine, it is easy to implement a function that builds the regularized loss function model (11.13).

Listing 11.9 Implementation of (11.13). Click here to download.

    // Model logistic regression (regularized with full 2-norm of theta)
    // X - n x d matrix of data points
    // y - length n vector classifying training points
    // lamb - regularization parameter
    public static double[] logisticRegression(Env        env,
                                              double[,]  X, 
                                              bool[]     y,
                                              double     lamb)
    {
      int n = X.GetLength(0);
      int d = X.GetLength(1);       // num samples, dimension

      using (Task task = new Task(env, 0, 0))
      {    
        // Variables [r; theta; t]
        int nvar = 1+d+n;
        task.appendvars(nvar);
        task.putvarboundsliceconst(0, nvar, boundkey.fr, -inf, inf);
        int r = 0, theta = 1, t = 1+d;

        // Objective lambda*r + sum(t)
        task.putobjsense(mosek.objsense.minimize);
        task.putcj(r, lamb);
        for(int i = 0; i < n; i++) 
          task.putcj(t+i, 1.0);

        // Softplus function constraints
        softplus(task, d, n, theta, t, X, y);

        // Regularization
        // Append a sequence of linear expressions (r, theta) to F
        long numafe = task.getnumafe();
        task.appendafes(1+d);
        task.putafefentry(numafe, r, 1.0);
        for(int i = 0; i < d; i++)
          task.putafefentry(numafe + i + 1, theta + i, 1.0);

        // Add the constraint
        task.appendaccseq(task.appendquadraticconedomain(1+d), numafe, null);

        // Solution
        task.optimize();
        return task.getxxslice(soltype.itr, theta, theta+d);
      }
    }

Example: 2D dataset fitting

In the next figure we apply logistic regression to the training set of 2D points taken from the example ex2data2.txt . The two-dimensional dataset was converted into a feature vector \(x\in\real^{28}\) using monomial coordinates of degrees at most 6.

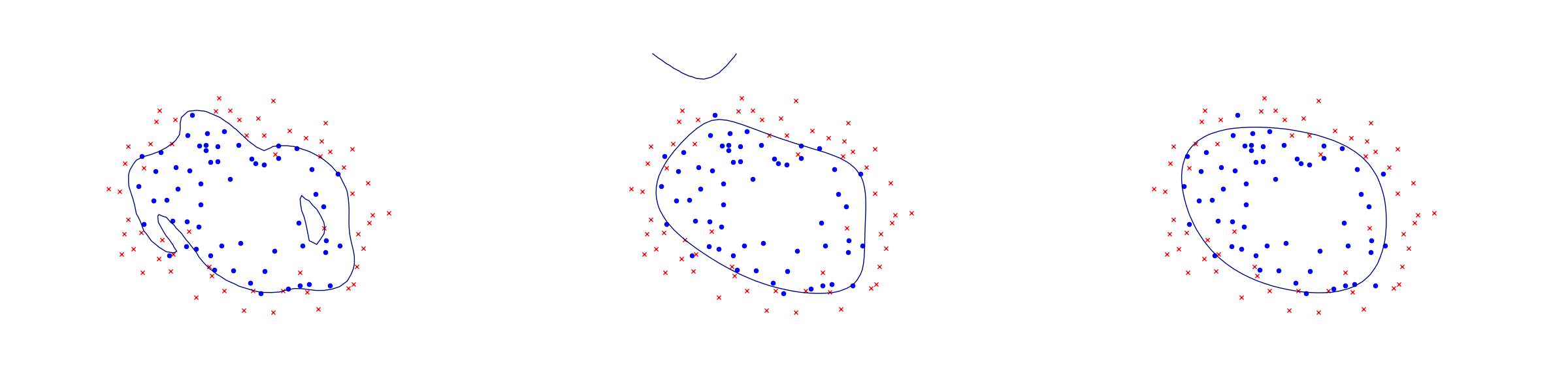
Fig. 11.2 Logistic regression example with none, medium and strong regularization (small, medium, large \(\lambda\)). Without regularization we get obvious overfitting.