A tutorial to MOSEK 10

KTH Royal Institute of Technology
Stockholm, May 19th, 2022

Sven Wiese

www.mosek.com

Outline

• Conic Optimization philosophy
• Standard cones with examples
• Further remarks / reading

Linear Programming

LP in standard form:

$ \begin{array}{ll} \mbox{minimize} & c^T x \\ \mbox{s.t.} & Ax = b\\ & x \geq 0. \end{array} $

Pro:

• Structure is explicit and simple.
• Data is simple: $c,A,b$.
• Structure implies data-independent convexity.
• Powerful duality theory including Farkas lemma.

Therefore, we have powerful algorithms and software.

Con:

• It is linear only.

Nonlinear Programming

The classical nonlinear optimization problem:

$ \begin{array}{ll} \mbox{minimize} & f(x)\\ \mbox{s.t.} & h(x) = 0 \\ & g(x) \leq 0. \end{array} $

Pro:

• It is very general.

Con:

• Structure is less explicit.
  • How to specify the problem at all in software?
  • How to compute gradients and Hessians if needed?
  • How to exploit structure?
• Smoothness?
• Verifying convexity is NP-hard!

Is there a class of optimization problems that

• allows to model nonlinearities,
• but preserves many of the good properties of Linear Programming?

Good partial orderings

Definition (Ben-Tal & Nemirovski, 2001): A good partial ordering of $\mathbb{R}^n$ is a vector relation that satisfies:

1. reflexivity
2. antisymmetry
3. transitivity
4. compatibility with linear operations

The coordinatewise ordering $$x\geq y \Longleftrightarrow x_i \geq y_i ~\forall i=1,\ldots,n$$

is an example, but not the only one!

• If for some good partial ordering $\succeq$ we define $$\mathcal{K}:=\{a\in\mathbb{R}^n~|~a\succeq 0\},$$ then $\mathcal{K}$ must be a pointed, convex cone:
  1. $a,a'\in \mathcal{K}\implies a+a'\in\mathcal{K}$
  2. $a\in\mathcal{K}, \lambda\geq 0\implies \lambda a\in\mathcal{K}$
  3. $a\in\mathcal{K}$ and $-a\in\mathcal{K}\implies a = 0$

• Conversely, if $\mathcal{K}$ is a non-empty pointed convex cone, then $x\succeq_{\mathcal{K}} y:\Longleftrightarrow x-y\in\mathcal{K}$ defines a good partial ordering.

The coordinatewise ordering leads to the cone $\mathbb{R}^n_+$.

Conic Programming

In standard form:

$ \begin{array}{ll} \mbox{minimize} & c^T x \\ \mbox{s.t.} & Ax = b\\ & x\in\mathcal{K} \end{array} $

where $\mathcal{K}$ is a (closed) pointed convex cone (with non-empty interior).

• Mixed Integer version straightforward: $x\in\mathcal{K}\cap\left(\mathbb{Z}^p\times\mathbb{R}^{n-p}\right)$
• (MI)LP is a special case!
• Typically, $\mathcal{K}=\mathcal{K}_1\times \mathcal{K}_2\times \cdots \times \mathcal{K}_{K}$ is a product of lower-dimensional cones.
• A conic building block $\mathcal{K}_i$ can be thought of as encoding some type of specific non-linearity.

The beauty of conic optimization

• Separation of data and structure:
  • Data: $c$, $A$ and $b$.
  • Structure: $\mathcal{K}$.
• No issues with smoothness and differentiability.
• Structural convexity.
• Duality (almost as in LP).

MOSEK

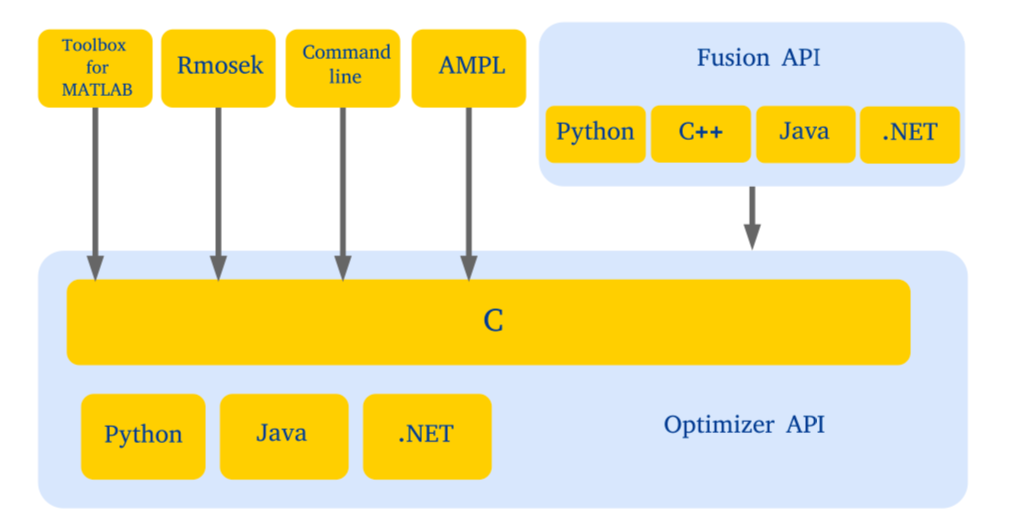
A software package/library for solving:

• Linear and conic problems.
• Convex quadratic and quadratically constrained problems.
• Also mixed-integer versions of the above.

Current version is MOSEK 10, released March 2022.

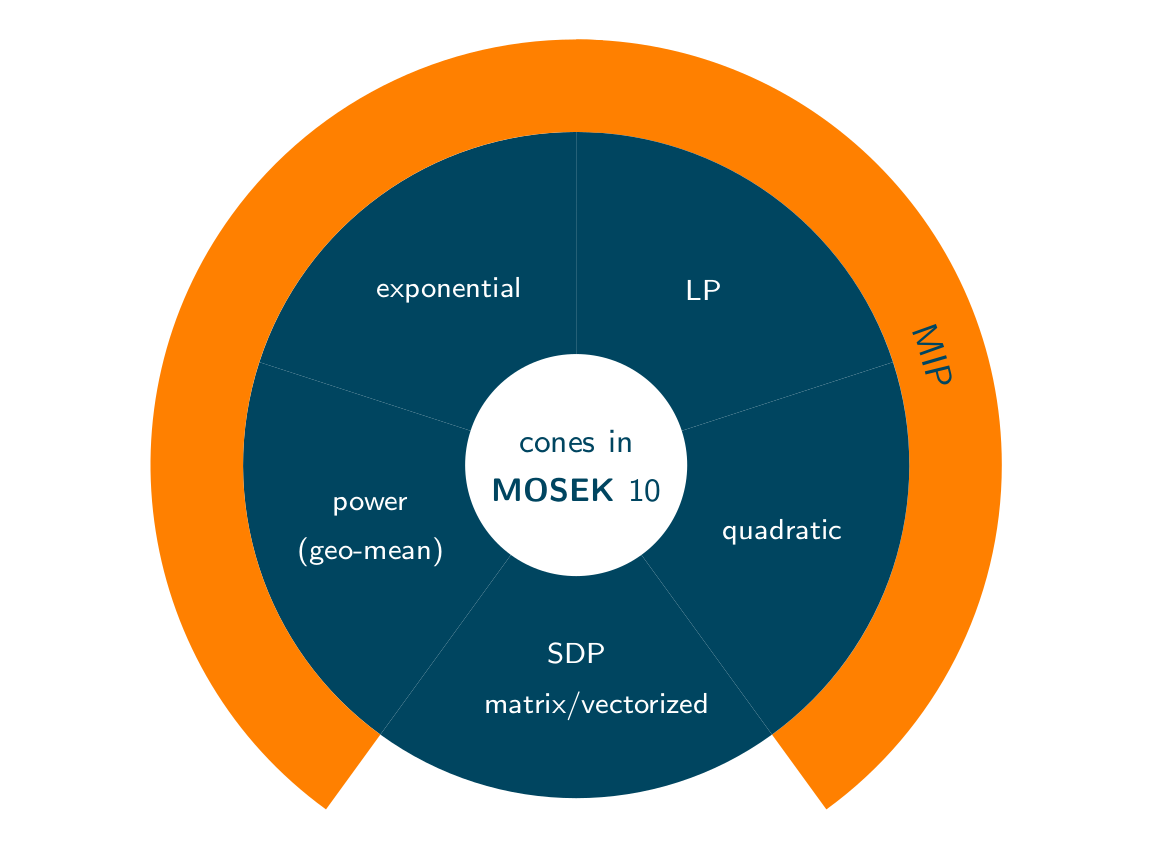
Continuous Optimmization folklore: "Almost all convex constraints that arise in practice are representable using these 5 cones."

More evidence: (Lubin et. al, 2016) show that all convex instances (333) in MINLPLIB2 are conic representable using only 4 of the above cones.

Interfaces to MOSEK

• Optimizer API: low-level, matrix-oriented, efficient

$ \begin{array}{lrcl} \\ \mbox{minimize} & & c^T x \\ \mbox{s.t.} & l^c \leq & Ax & \leq u^c\\ & l^x \leq & x & \leq u^x\\ & & Fx + g & \in \mathcal{K} \end{array} $

• Fusion API: object-oriented, specifically for conic optimization

from mosek.fusion import *

print("Using Mosek version {ver}".format(ver=Model.getVersion()))

Using Mosek version 10.0.12

Linear Programming case study

Solve a simple diet problem: combine servings of meals to meat min/max nutrient requirements.

	Corn	Milk	Bread
Cost per serving	\$0.18	\$0.23	\$0.05
Vitamin A	107	500	0
Calories	72	121	65
Max servings	-	10	10

Vitamin A should stay between 2,000 and 2,250, calories between 5,000 and 50,000.

c, ux, lc, uc

([0.18, 0.23, 0.05], [inf, 10, 10], [5000, 2000], [50000, 2250])

np.reshape(A, (2,3))

array([[107, 500,   0],
       [ 72, 121,  65]])

First create a model:

m = Model("diet-LP")

Add variables to it:

x = m.variable("x", 3, Domain.greaterThan(0.0))

Set the objective:

m.objective("obj", ObjectiveSense.Minimize, Expr.dot(c, x))

Add constraints on vitamin A and calorie intake:

m.constraint("vitaminA", Expr.dot(A[0], x), Domain.inRange(lc[0], uc[0]))
m.constraint("calories", Expr.dot(A[1], x), Domain.inRange(lc[1], uc[1]));

Set upper bounds on variables:

m.constraint(x.index(1), Domain.lessThan(ux[1]))
m.constraint(x.index(2), Domain.lessThan(ux[2]));

And solve:

m.solve()

# Always check the status
print(m.getPrimalSolutionStatus())

# Actual solution values
solvals = x.level()

print("Optimal x = {}".format(solvals))
print("Cost = {}".format(m.primalObjValue()))

SolutionStatus.Optimal
Optimal x = [ 1.94444444 10.         10.        ]
Cost = 3.1499999999999995

Try some linear Algebra utils:

m.constraint("allIntakes", Expr.mul(A, x), Domain.inRange(lc, uc));

m.solve()
print(m.getPrimalSolutionStatus())
print("Cost = {}".format(m.primalObjValue()))

SolutionStatus.Optimal
Cost = 3.1500000000000004

# clear the model
m.dispose()

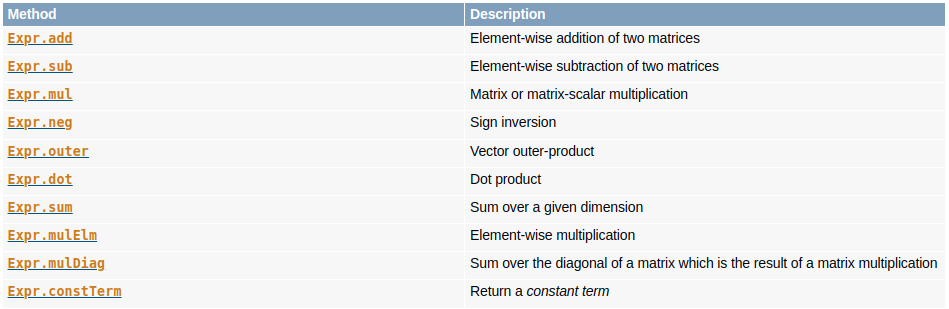
Linear operators available in Fusion's Expr class:

Quadratic Cone Programming

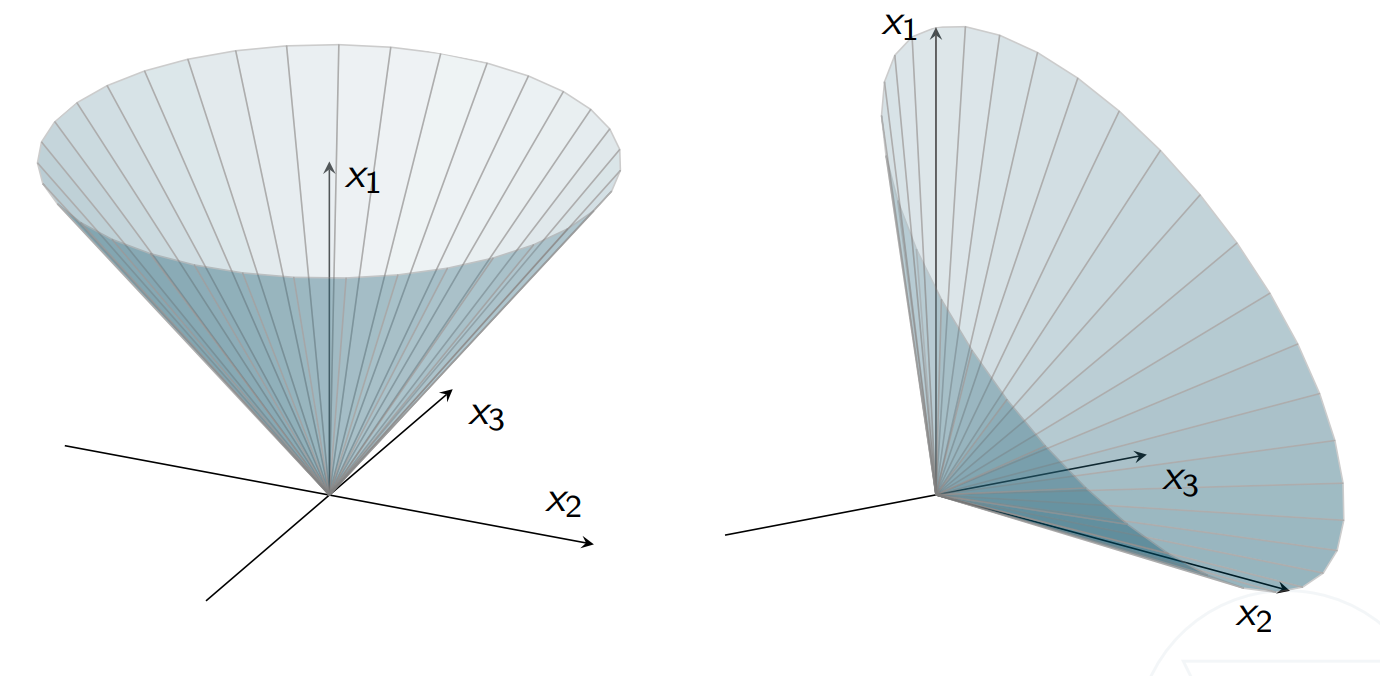
The quadratic cone family:

• the quadratic cone

$ \mathcal{Q}^n = \{ x\in \mathbb{R}^n \mid x_1 \geq \left( x_2^2 + \cdots + x_n^2 \right)^{1/2} = \|x_{2:n}\|_2 \} $

• the rotated quadratic cone

$ \mathcal{Q}_r^n = \{ x\in \mathbb{R}^n \mid 2x_1 x_2 \geq x_3^2 + \cdots + x_n^2 = \|x_{3:n}\|_2^2, \, x_1, x_2\geq 0\} $

Are equivalent in the sense that $x\in\mathcal{Q}^n\Longleftrightarrow T_nx\in \mathcal{Q}^n_r$ with $T_n = $ $ \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} & 0\\ 1/\sqrt{2} & -1/\sqrt{2} & 0\\ 0 & 0 & I_{n-2} \end{pmatrix}. $

Conic quadratic modeling

• Second-order cone inequality:

$ c^Tx + d \geq \| Ax + b\|_2 \quad \Longleftrightarrow \quad (c^Tx + d, Ax+b) \in \mathcal{Q}^{m+1} $

• Squared Euclidean norm:

$ t\geq\| x \|_2^2 \quad \Longleftrightarrow \quad (t, 1/2, x) \in \mathcal{Q}_r^{n+2} $

• Convex quadratic inequality:

$ t\geq (1/2)x^T Q x \quad \Longleftrightarrow \quad (t, 1, F^Tx) \in \mathcal{Q}_r^{k+2}\text{ with }Q=F^TF, F\in\mathbb{R}^{n\times k}. $

Any convex (MI)QCQP can be cast in conic form!

Conic quadratic case study: least squares regression

Simplest form: given observations $y\in\mathbb{R}^n$ and features $X\in\mathbb{R}^{n\times d}$, solve

$ \min_{w\in\mathbb{R}^d}\Vert y - Xw\Vert_2 $

Put it in the conic framework - we need a bit of reformulation:

$ \begin{array}{lrcl} \\ \mbox{minimize} & & c^T x \\ \mbox{s.t.} & l^c \leq & Ax & \leq u^c\\ & l^x \leq & x & \leq u^x\\ & & Fx + g & \in \mathcal{K} \end{array} $

Remember: $\mathcal{Q}^n = \{ x\in \mathbb{R}^n \mid x_1 \geq \left( x_2^2 + \cdots + x_n^2 \right)^{1/2} = \|x_{2:n}\|_2 \}$

Solution:

• Make the objective linear:

$ \begin{array}{ll} \mbox{minimize} & t\\ \mbox{s.t.} & t\geq\Vert y-Xw\Vert_2 \\ & t\in\mathbb{R}, w\in\mathbb{R}^d \end{array} $

• Use conic notation:

$ \begin{array}{ll} \mbox{minimize} & t\\ \mbox{s.t.} & (t, y-Xw)\in \mathcal{Q}^{n+1}\\ & t\in\mathbb{R}, w\in\mathbb{R}^d \end{array} $

plt.scatter(s,y);

n = len(s)
n

100

X = [[1,t,t**2,t**3] for t in s]
d = len(X[0])
d

4

m = Model("lse")

The regression coefficients and bound on the norm:

w = m.variable("w", d)
t = m.variable("t")

The quadratic cone constraint, note the (vertical) stacking:

r = Expr.sub(y, Expr.mul(X,w))
m.constraint(Expr.vstack(t, r), Domain.inQCone());

The objective:

m.objective(ObjectiveSense.Minimize, t)

m.solve()
print(m.getPrimalSolutionStatus())

SolutionStatus.Optimal

solvals = w.level()
ticks = np.linspace(0, 1, 100)
plt.scatter(s,y)
plt.plot(ticks, sum([solvals[i]*ticks**i for i in range(4)]), 'k', color='red');

# clear the model
m.dispose()

Advanced conic quadratic modeling: simple rational powers

Portfolio optimization with market impact:

$ \begin{array}{ll} \mbox{maximize} & \mu^Tx\\ \mbox{s.t.} & \sum_ix_i \color{red}{+ a^Tt} = 1 \\ & \color{red}{t_i = x_i^{3/2}\qquad\forall i}\\ & x^T\Sigma x \leq \sigma^2 \\ & x \geq 0 \end{array} $

$x^t\Sigma x\leq \sigma^2$ is convex quadratic (easy to reformulate...), but how to model $t_i\geq x_i^{3/2}$?

For some constant $c$, together with $x\geq 0$,

$ (s,t,x), (x,c,s)\in\mathcal{Q}_r^3, s\in\mathbb{R} $

implies $t_i \geq x_i^{3/2}$.

What's the value of $c$? Remember:

$ \mathcal{Q}_r^n = \{ x\in \mathbb{R}^n \mid 2x_1 x_2 \geq x_3^2 + \cdots + x_n^2 = \|x_{3:n}\|_2^2, \, x_1, x_2\geq 0\} $

Solution:

$ (s,t,x), (x,1/8,s)\in\mathcal{Q}_r^3\implies 2st\geq x^2, 2x\cdot\frac{1}{8}\geq s^2 $

$ \implies 4s^2t^2\cdot 2x\cdot \frac{1}{8}\geq x^4\cdot s^2\implies t^2\geq x^3\implies t\geq x^{3/2} $

# rqcone syntax
m.constraint(Expr.vstack(s, t, x), Domain.inRotatedQCone());

Symmetric vs Nonsymmetric cones

The LP and the quadratic cones are so-called symmetric cones: they are homogeneous and self-dual.

There are several nonsymmetric cones, exponential and power cones being two examples.

• Symmetric cones (LP, quadratic, SDP) have been available in MOSEK for many years.
• Nonsymmetric cone support (power, exp) since version 9 (2019).

Power Cone Programming

$n$-dimensional power cone:

$ \mathcal{P}^\alpha_n = \{ x\in\mathbb{R}^n \mid x_1^\alpha x_2^{(1-\alpha)} \geq \left( x_3^2 + \cdots + x_n^2 \right)^{1/2} = \|x_{3:n}\|_2, \: x_1, x_2 \geq 0 \} $

with parameter $0 < \alpha < 1$.

More generally:

$ \mathcal{P}^{(\alpha_1, \ldots, \alpha_{n_l})}_n = \{ x\in\mathbb{R}^n \mid \prod_\limits{i=1}^{n_l} x_i^{\beta_i} \geq \left( x_{n_l+1}^2 + \cdots + x_n^2 \right)^{1/2} = \|x_{n_l+1:n}\|_2, \: x_1,\ldots, x_{n_l} \geq 0 \} $

where $\beta_i = \alpha_i / (\sum_j\alpha_j)$.

Power cone modeling

• Simple powers:

$ |t| \leq x^p, x \geq 0 \text{ with } 0 < p < 1 \Longleftrightarrow (x, 1, t)\in\mathcal{P}_3^{p} $

• similar: $ t \geq |x|^p \text{ with } p > 1 $

• Geometric mean:

$ (x_1\cdots x_n)^{1/n}\geq|z| \Longleftrightarrow (x,z)\in\mathcal{P}_{n+1}^{(1/n, \ldots,1/n)} $

• $p$-norms, ...

Power cone case study: Portfolio optimization with market impact

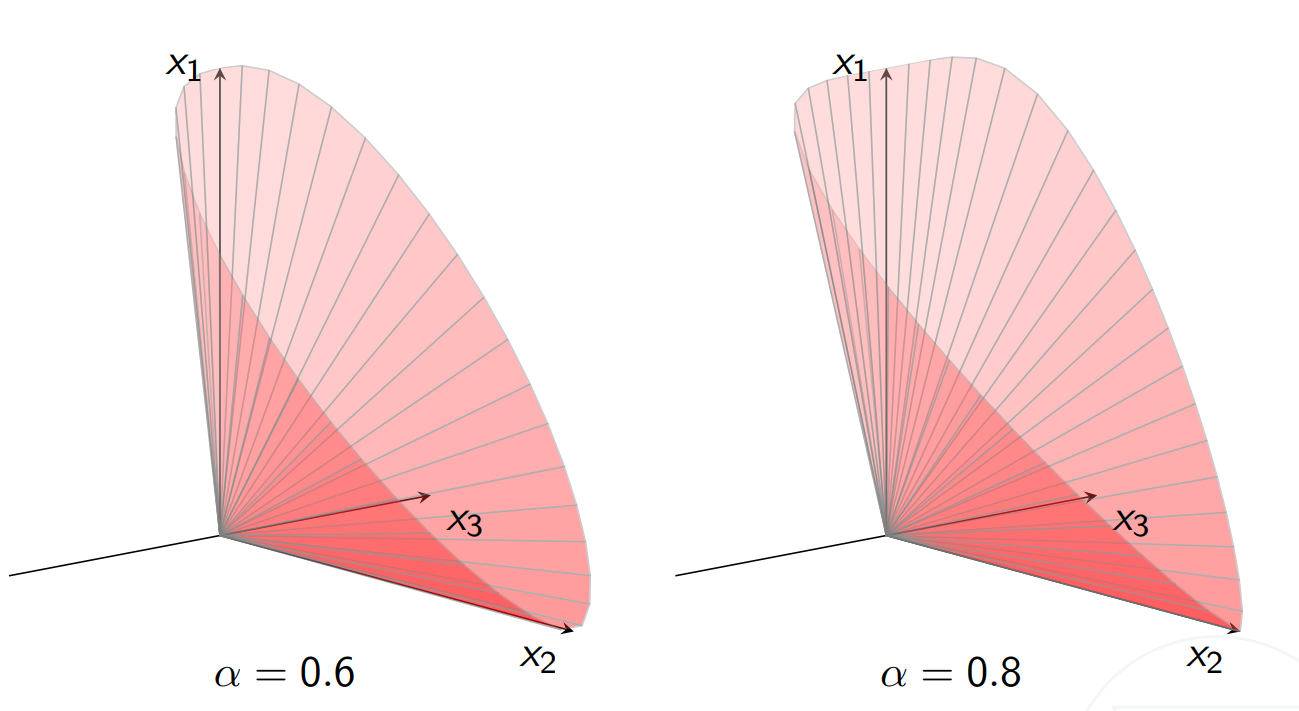
From above:

$ \begin{array}{ll} \mbox{maximize} & \mu^Tx\\ \mbox{s.t.} & \sum_ix_i + a^Tt = 1 \\ & t_i = x_i^{3/2}\qquad\forall i\\ & x^T\Sigma x \leq \sigma^2 \\ & x \geq 0 \end{array} $

For $t \geq x^{3/2}$ use the power cone (instead of $(s,t,x), (x,1/8,s)\in \mathcal{Q}_r^3$...). Remember:

$$ \mathcal{P}^\alpha_3 = \{ x\in\mathbb{R}^3 \mid x_1^\alpha x_2^{(1-\alpha)} \geq | x_3|, \: x_1, x_2 \geq 0 \} $$

Solution: $$t \geq |x|^{3/2} \Longleftrightarrow (t,1,x)\in\mathcal{P}_3^{(2/3,1/3)}.$$

nassets, sigma**2, mu

(8,
 0.049999999999999996,
 [0.072, 0.1552, 0.1754, 0.0898, 0.429, 0.3929, 0.3217, 0.1838])

S

[[0.0946, 0.0374, 0.0349, 0.0348, 0.0542, 0.0368, 0.0321, 0.0327],
 [0.0374, 0.0775, 0.0387, 0.0367, 0.0382, 0.0363, 0.0356, 0.0342],
 [0.0349, 0.0387, 0.0624, 0.0336, 0.0395, 0.0369, 0.0338, 0.0243],
 [0.0348, 0.0367, 0.0336, 0.0682, 0.0402, 0.0335, 0.0436, 0.0371],
 [0.0542, 0.0382, 0.0395, 0.0402, 0.1724, 0.0789, 0.07, 0.0501],
 [0.0368, 0.0363, 0.0369, 0.0335, 0.0789, 0.0909, 0.0536, 0.0449],
 [0.0321, 0.0356, 0.0338, 0.0436, 0.07, 0.0536, 0.0965, 0.0442],
 [0.0327, 0.0342, 0.0243, 0.0371, 0.0501, 0.0449, 0.0442, 0.0816]]

m = Model("portfolio")

x = m.variable("x", nassets, Domain.greaterThan(0.0))
t = m.variable("t", nassets, Domain.unbounded())

Budget constraint $\sum_ix_i + a^Tt = 1$:

a = 0.01 # same weight for all assets
lhs = Expr.add(Expr.sum(x), Expr.mul(a, Expr.sum(t)))
m.constraint('budget', lhs, Domain.equalsTo(1));

One power cone constraint for each asset: $(t_i, 1, x_i) \in\mathcal{P}_3^{(2/3,1/3)}$

for i in range(nassets):
    stack = Expr.hstack(Expr.hstack(t.index(i), 1), x.index(i))
    m.constraint('market_' + str(i), stack, Domain.inPPowerCone(2/3))
    # equivalent: Domain.inPPowerCone([2/3, 1/3])

Equivalent vectorization:

stack = Expr.hstack(Expr.hstack(t, Expr.constTerm(nassets, 1)), x)
m.constraint('market', stack, Domain.inPPowerCone(2/3));

The convex quadratic risk constraint $x^T\Sigma x \leq \sigma^2$:

G = np.linalg.cholesky(S)
print(np.max(np.abs(S - G @ G.T)))

1.3877787807814457e-17

m.constraint('risk', Expr.vstack(sigma, Expr.mul(G.T, x)), Domain.inQCone());

Set objective and solve:

m.objective('max-return', ObjectiveSense.Maximize, Expr.dot(mu, x))

m.solve()
print(m.getPrimalSolutionStatus())
solvals = x.level()
print("Optimal x = {}".format(solvals))

SolutionStatus.Optimal
Optimal x = [1.03736753e-09 4.65082276e-09 4.82745337e-08 1.33397513e-09
 9.53155147e-02 5.12895846e-01 1.93241136e-01 3.10401104e-09]

# clear the model
m.dispose()

Exponential Cone Programming

The exponential cone: closure of the epigraph of the perspective of the exponential function:

$ \mathcal{K}_{exp} := \text{cl}\{ x\in\mathbb{R}^3 \mid x_1 \geq x_2 \exp(x_3/x_2), \: x_2 > 0 \} $

or more explicitly

$ \mathcal{K}_{exp} = \{ (x_1, x_2, x_3) \mid x_1 \geq x_2 \exp(x_3/x_2), \: x_2 > 0 \}\bigcup\{(x_1, 0, x_3) \mid x_1 \geq 0, x_3\leq 0\} $

Exponential cone modeling

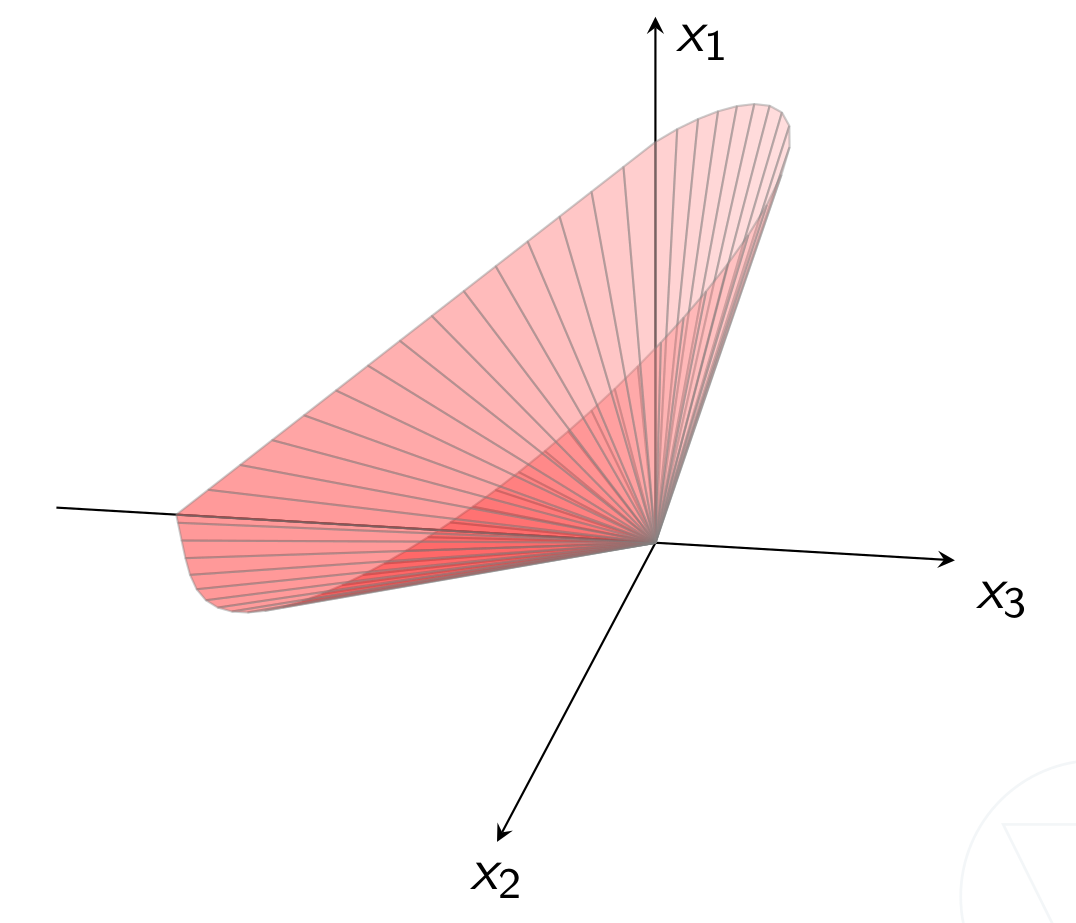
• Exponentials:

  $ t\geq e^x \quad \Longleftrightarrow \quad (t,1,x)\in \mathcal{K}_{exp} $

• Logarithm:

  $ \log x \geq t \quad \Longleftrightarrow \quad (x,1,t)\in \mathcal{K}_{exp} $

• Entropy:

  $ -x \log x \geq t \quad \Longleftrightarrow \quad (1,x,t)\in \mathcal{K}_{exp} $

• ...

Exponential cone case study: logistic regression

Given $n$ binary-labeled training-points $\{ (x_i, y_i) \}$ in $\mathbb{R}^{d+1}$, determine the classifier

$ h_\theta(x) = \frac{1}{1+\exp(-\theta^T x)} $

$\approx$ "probability that $x$ belongs to class 1".

Log-likelihood training:

$ \begin{array}{lll} \mbox{minimize} & \sum_i t_i \\ \mbox{s.t.} & t_i \geq \log( 1 + \exp(-\theta^T x_i)), & y_i = 1\\ & t_i \geq \log( 1 + \exp(\theta^T x_i)), & y_i = 0\\ & \theta\in\mathbb{R}^d \end{array} $

How to model the softplus function $t\geq\log(1+\exp(z))$?

Hint: write as $e^{\ldots} + e^{\ldots} \leq 1$ and use 2 cone constraints as in

$ e^x\leq t \quad \Longleftrightarrow \quad (t,1,x)\in \mathcal{K}_{exp} $

Solution: $$ u + v \leq 1, (u,1,z-t), (v,1,-t)\in\mathcal{K}_{exp}\implies e^{z-t} + e^{-t} \leq u + v \leq 1 $$

$$ \implies e^t\geq 1 + e^z\implies t\geq\log(1+\exp(z)) $$

# 2d points p with labels
pos = np.where(labels == 1)
neg = np.where(labels == 0)
plt.scatter(p[pos,0], p[pos,1], marker='o', color='b')
plt.scatter(p[neg,0], p[neg,1], marker='x', color='r');

n = len(p)
n

118

Take monomials with some max degree $D$ as features: $$\theta^T x_i = \sum_{(a,b)~:~a+b\leq D}\theta_{(a,b)}p_{i1}^ap_{i2}^b$$

# map 2d data through all monomials of degree <= D
def mapFeature(p, D):
    return np.array([(p[0]**a)*(p[1]**b) for a,b in itertools.product(range(D+1),
                                                       range(D+1)) if a+b<=D])

# store features of all observations in matrix P
P = np.array([mapFeature(a, 6) for a in p])
d = P.shape[1]
d

28

m = Model("log-reg")

theta = m.variable("theta", d)
t = m.variable("t", n)                

# imposes t >= log(1 + exp(z)) with exponential cones
def softplus(m, t, z):
    
    uv = m.variable(2)
    m.constraint(Expr.sum(uv), Domain.lessThan(1))
    
    stack = Expr.hstack(uv, Expr.constTerm(2, 1), Expr.vstack(Expr.sub(z,t), Expr.neg(t)))
    m.constraint(stack, Domain.inPExpCone())

for i in range(n):
    dot = Expr.dot(P[i], theta)
    softplus(m, t.index(i), Expr.neg(dot) if labels[i] == 1 else dot)

m.objective(ObjectiveSense.Minimize, Expr.sum(t))

m.solve()
print(m.getPrimalSolutionStatus())

SolutionStatus.Optimal

u = np.linspace(-1, 1, 50)
v = np.linspace(-1, 1, 50)
w = np.zeros(shape=(len(u), len(v)))
for i in range(len(u)):
    for j in range(len(v)):
        w[i,j] = np.dot(mapFeature([u[i],v[j]], 6), theta.level())
plt.contour(u, v, w.T, [0])
plt.scatter(p[pos,0], p[pos,1], marker='o', color='b')
plt.scatter(p[neg,0], p[neg,1], marker='x', color='r');

Algorithms employed by MOSEK

• Simplex algorithms (primal/dual) available for LPs
• Interior-point optimizer, used on conic problems (default choice also for LP)
• (Conic) Branch-and-Bound for MIP
• Conic Outer-Approximation for conic MIP

The interior-point optimizer log:

m.setLogHandler(sys.stdout)
m.setSolverParam("logCutSecondOpt", 0)
m.solve()

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries                  : 1                 time                   : 0.00            
Lin. dep.  - tries                  : 1                 time                   : 0.00            
Lin. dep.  - number                 : 0               
Presolve terminated. Time: 0.01    
Problem
  Name                   : log-reg         
  Objective sense        : minimize        
  Type                   : CONIC (conic optimization problem)
  Constraints            : 118             
  Affine conic cons.     : 236             
  Disjunctive cons.      : 0               
  Cones                  : 0               
  Scalar variables       : 383             
  Matrix variables       : 0               
  Integer variables      : 0               

Optimizer  - threads                : 2               
Optimizer  - solved problem         : the primal      
Optimizer  - Constraints            : 236
Optimizer  - Cones                  : 237
Optimizer  - Scalar variables       : 737               conic                  : 737             
Optimizer  - Semi-definite variables: 0                 scalarized             : 0               
Factor     - setup time             : 0.00              dense det. time        : 0.00            
Factor     - ML order time          : 0.00              GP order time          : 0.00            
Factor     - nonzeros before factor : 7257              after factor           : 7257            
Factor     - dense dim.             : 0                 flops                  : 9.65e+05        
ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  
0   1.6e+00  1.3e+00  2.9e+02  0.00e+00   9.768493109e+01   -1.900040724e+02  1.0e+00  0.02  
1   9.6e-01  7.8e-01  1.4e+02  6.66e-01   8.076910687e+01   -1.038898401e+02  6.0e-01  0.04  
2   2.5e-01  2.1e-01  2.0e+01  7.36e-01   5.434773100e+01   1.360436002e-01   1.6e-01  0.05  
3   7.9e-02  6.5e-02  3.8e+00  9.00e-01   4.401162601e+01   2.603100765e+01   5.0e-02  0.05  
4   3.8e-02  3.1e-02  1.4e+00  8.77e-01   3.942023948e+01   3.017437637e+01   2.4e-02  0.05  
5   1.4e-02  1.2e-02  3.6e-01  8.43e-01   3.611469451e+01   3.223559751e+01   9.1e-03  0.05  
6   8.2e-03  6.7e-03  1.7e-01  7.17e-01   3.440135253e+01   3.187669380e+01   5.2e-03  0.06  
7   3.7e-03  3.0e-03  5.9e-02  7.46e-01   3.311358979e+01   3.182690311e+01   2.3e-03  0.06  
8   2.6e-03  2.1e-03  3.7e-02  7.42e-01   3.268713391e+01   3.172940015e+01   1.6e-03  0.06  
9   1.3e-03  1.1e-03  1.5e-02  6.65e-01   3.193726078e+01   3.137467986e+01   8.2e-04  0.06  
10  1.0e-03  8.4e-04  1.2e-02  4.78e-01   3.162516073e+01   3.111691947e+01   6.5e-04  0.07  
11  5.4e-04  4.4e-04  6.8e-03  2.07e-01   3.057871447e+01   3.016602404e+01   3.4e-04  0.08  
12  3.4e-04  2.8e-04  4.4e-03  8.17e-02   2.991192644e+01   2.957046429e+01   2.2e-04  0.08  
13  2.3e-04  1.9e-04  3.0e-03  4.66e-02   2.933960273e+01   2.905411004e+01   1.5e-04  0.09  
14  1.7e-04  1.4e-04  2.1e-03  9.36e-02   2.893584448e+01   2.869792152e+01   1.1e-04  0.09  
15  1.0e-04  8.4e-05  1.2e-03  9.89e-02   2.818628233e+01   2.800468820e+01   6.5e-05  0.09  
16  3.3e-05  2.7e-05  3.2e-04  2.27e-01   2.699551891e+01   2.691484907e+01   2.1e-05  0.09  
17  1.1e-05  8.8e-06  7.3e-05  5.06e-01   2.634393282e+01   2.631216522e+01   6.8e-06  0.10  
18  3.7e-06  3.0e-06  1.6e-05  7.54e-01   2.606416024e+01   2.605230274e+01   2.4e-06  0.10  
19  8.1e-07  6.6e-07  1.7e-06  8.71e-01   2.591882345e+01   2.591612126e+01   5.1e-07  0.10  
20  1.8e-07  1.5e-07  1.8e-07  9.72e-01   2.588558641e+01   2.588498745e+01   1.1e-07  0.11  
21  5.1e-08  4.1e-08  2.8e-08  9.95e-01   2.587890900e+01   2.587873929e+01   3.2e-08  0.11  
22  9.1e-09  7.2e-09  2.0e-09  9.99e-01   2.587672670e+01   2.587669725e+01   5.5e-09  0.11  
23  4.0e-09  1.9e-09  2.9e-10  1.00e+00   2.587638933e+01   2.587638141e+01   1.5e-09  0.11  
24  1.2e-09  3.3e-10  2.0e-11  1.00e+00   2.587628841e+01   2.587628706e+01   2.6e-10  0.12  
25  1.4e-09  3.1e-10  1.9e-11  1.00e+00   2.587628742e+01   2.587628613e+01   2.4e-10  0.12  
26  1.5e-09  2.5e-10  1.4e-11  1.00e+00   2.587628363e+01   2.587628258e+01   2.0e-10  0.12  
27  1.3e-09  1.6e-10  6.8e-12  1.00e+00   2.587627742e+01   2.587627677e+01   1.2e-10  0.13  
28  4.6e-10  3.3e-11  6.4e-13  1.00e+00   2.587626940e+01   2.587626927e+01   2.5e-11  0.13  
Optimizer terminated. Time: 0.14    


Interior-point solution summary
  Problem status  : PRIMAL_AND_DUAL_FEASIBLE
  Solution status : OPTIMAL
  Primal.  obj: 2.5876269399e+01    nrm: 4e+03    Viol.  con: 8e-09    var: 0e+00    acc: 7e-10  
  Dual.    obj: 2.5876269265e+01    nrm: 1e+00    Viol.  con: 0e+00    var: 5e-09    acc: 0e+00  

The interior-point optimizer solves the so-called homogeneous model, and converges towards

• primal feasibility
• dual feasibility
• and optimality

at the same time!

... or otherwise provides certificates of primal or dual infeasibility (modulo ill-posedness).

Integer variables

MOSEK allows integer variables together with all cone types seen until now.

Example: Logistic regression problem as above with feature selection:

$ \begin{array}{lll} \mbox{minimize} & \sum_i t_i {\color{red}{~+~ F\cdot\lvert\{j~|~\theta_j \neq 0\}\rvert}}\\ \mbox{s.t.} & t_i \geq \log( 1 + \exp(-\theta^T x_i)), & y_i = 1\\ & t_i \geq \log( 1 + \exp(\theta^T x_i)), & y_i = 0\\ & \theta\in\mathbb{R}^d \end{array} $

Modeled with bigM-constraints:

$ \begin{array}{lll} \mbox{minimize} & \sum_i t_i {\color{red}{~+~ F\cdot\sum_jz_j}}\\ \mbox{s.t.} & t_i \geq \log( 1 + \exp(-\theta^T x_i)), & y_i = 1\\ & t_i \geq \log( 1 + \exp(\theta^T x_i)), & y_i = 0\\ & {\color{red}{-Mz_j\leq\theta_j \leq Mz_j}}&{\color{red}{\forall j}}\\ & {\color{red}{z_j\in\{0,1\}^d}}\\ & \theta\in\mathbb{R}^d \end{array} $

z = m.variable(d, Domain.binary())

bigM = 10    
m.constraint(Expr.add(theta, Expr.mul(bigM, z)), Domain.greaterThan(0.0))
m.constraint(Expr.add(Expr.neg(theta), Expr.mul(bigM, z)), Domain.greaterThan(0.0))
    
F = 1.0
m.updateObjective(Expr.mul(F, Expr.sum(z)), z)

m.solve()
print(m.getPrimalSolutionStatus())

Optimizer started.
Mixed integer optimizer started.
Threads used: 2
Presolve started.
Presolve terminated. Time = 0.02, probing time =  0.00
Presolved problem: 764 variables, 292 constraints, 3862 non-zeros
Presolved problem: 0 general integer, 28 binary, 736 continuous
Presolved problem: 236 cones
Clique table size: 0
BRANCHES RELAXS   ACT_NDS  DEPTH    BEST_INT_OBJ         BEST_RELAX_OBJ       REL_GAP(%)  TIME  
0        1        1        0        5.3697611392e+01     4.4304292152e+01     17.49       0.1   
0        1        1        0        5.1548852184e+01     4.4304292152e+01     14.05       0.4   
Cut generation started.
0        1        1        0        5.1548852184e+01     4.4304292035e+01     14.05       0.7   
0        2        1        0        5.1548852184e+01     4.4469465482e+01     13.73       0.8   
Cut generation terminated. Time = 0.24
7        12       8        4        5.0897036500e+01     4.4487982131e+01     12.59       1.3   
15       20       14       5        4.9813496885e+01     4.5353208028e+01     8.95        1.5   
29       34       24       6        4.9813496885e+01     4.5353208028e+01     8.95        1.7   
53       58       40       9        4.9400237093e+01     4.6006341562e+01     6.87        2.1   
93       98       64       12       4.8587817063e+01     4.6458428636e+01     4.38        2.7   
139      143      88       15       4.8179334094e+01     4.6657335927e+01     3.16        3.4   
192      189      87       8        4.7152850707e+01     4.7152850707e+01     0.00e+00    4.0   
An optimal solution satisfying the relative gap tolerance of 1.00e-02(%) has been located.
The relative gap is 0.00e+00(%).
An optimal solution satisfying the absolute gap tolerance of 0.00e+00 has been located.
The absolute gap is 0.00e+00.

Objective of best integer solution : 4.715285070663e+01      
Best objective bound               : 4.715285070663e+01      
Initial feasible solution objective: Undefined
Construct solution objective       : Not employed
User objective cut value           : Not employed
Number of cuts generated           : 2
  Number of CMIR cuts              : 2
Number of branches                 : 192
Number of relaxations solved       : 189
Number of interior point iterations: 4508
Number of simplex iterations       : 0
Time spend presolving the root     : 0.02
Time spend optimizing the root     : 0.03
Mixed integer optimizer terminated. Time: 4.00

Optimizer terminated. Time: 4.01    


Integer solution solution summary
  Problem status  : PRIMAL_FEASIBLE
  Solution status : INTEGER_OPTIMAL
  Primal.  obj: 4.7152850707e+01    nrm: 2e+01    Viol.  con: 6e-09    var: 0e+00    acc: 8e-09    itg: 3e-07  
SolutionStatus.Optimal

print("Selected {s} out of {t} features.".format(s = int(sum(z.level())), t = z.getSize()))
u = np.linspace(-1, 1, 50)
v = np.linspace(-1, 1, 50)
w = np.zeros(shape=(len(u), len(v)))
for i in range(len(u)):
    for j in range(len(v)):
        w[i,j] = np.dot(mapFeature([u[i],v[j]], 6), theta.level())
plt.contour(u, v, w.T, [0])
plt.scatter(p[pos,0], p[pos,1], marker='o', color='b')
plt.scatter(p[neg,0], p[neg,1], marker='x', color='r');

Selected 7 out of 28 features.

Semidefinite Programming

The PSD cone can be defined in matrix space $\mathbb{R}^{n\times n}$:

$ \mathbb{S}^n_+ := \{ X\in \mathbb{R}^{n\times n} \mid X\in\mathbb{S}^n, z^T X z \geq 0, \: \forall z \in\mathbb{R}^n \} $

If desired one may also work in vector space $\mathbb{R}^{n(n+1)/2}$:

$ \mathcal{S}^{n(n+1)/2} := \{ x\in \mathbb{R}^{n(n+1)/2} \mid x = \text{svec}(X)~\forall X\in\mathbb{S}_+^n\} $

with $ \text{svec}(X) := (X_{11}, \sqrt{2}X_{21}, \ldots, \sqrt{2}X_{n1}, X_{22}, \sqrt{2}X_{32}, \ldots, X_{nn})^T $

Note that $\Vert X\Vert_F = \Vert \text{svec}(X)\Vert_2$.

• MOSEK Fusion supports modeling with $\mathbb{S}^n_+$.
• The optimizer API allows both $\mathbb{S}^n_+$ and $\mathcal{S}^{n(n+1)/2}$.

SDP case study: nearest correlation matrix

Let $C\in\mathbb{S}^n$ and assume we want to find its nearest correlation matrix

$ X^*\in\mathcal{C}:=\{X\in\mathbb{S}^n_+~|~X_{ii} = 1 ~\forall i=1,\ldots, n\}, $

i.e. $X^* = \min_{X\in\mathcal{C}}\Vert C - X\Vert_F.$

$ \begin{array}{ll} \mbox{minimize} & t\\ \mbox{s.t.} & (t, \text{svec}(C-X))\in\mathcal{Q}^{n(n+1)/2 + 1} \\ & \text{diag}(X) = e\\ & X\in \mathbb{S}^{n}_+. \end{array} $

n = np.shape(C)[0]
n, C

(5,
 [[0.0, 0.5, -0.1, -0.2, 0.5],
  [0.5, 1.25, -0.05, -0.1, 0.25],
  [-0.1, -0.05, 0.51, 0.02, -0.05],
  [-0.2, -0.1, 0.02, 0.54, -0.1],
  [0.5, 0.25, -0.05, -0.1, 1.25]])

def svec(X):
    N = X.getShape()[0]

    msubi = range(N * (N + 1) // 2)
    msubj = [i * N + j for i in range(N) for j in range(i + 1)]
    mcof  = [2.0**0.5 if i !=
             j else 1.0 for i in range(N) for j in range(i + 1)]

    S = Matrix.sparse(N * (N + 1) // 2, N * N, msubi, msubj, mcof)
    return Expr.mul(S, Expr.flatten(X))

m = Model("corr-mat")

# use a matrix variable!
X = m.variable("X", [n,n], Domain.inPSDCone(n))
t = m.variable("t")

# (t, vec (C-X)) \in Q
m.constraint("norm", Expr.vstack(t, svec(Expr.sub(C, X))), Domain.inQCone());

# diag(X) = e
m.constraint("diag", X.diag(), Domain.equalsTo(1.0));

m.objective(ObjectiveSense.Minimize, t)

m.solve()
print(m.getPrimalSolutionStatus())

SolutionStatus.Optimal

X.level(), C

(array([ 1.        ,  0.50000348, -0.10000045, -0.20000096,  0.50000348,
         0.50000348,  1.        , -0.04999996, -0.09999996,  0.25000085,
        -0.10000045, -0.04999996,  1.        ,  0.01999993, -0.04999996,
        -0.20000096, -0.09999996,  0.01999993,  1.        , -0.09999996,
         0.50000348,  0.25000085, -0.04999996, -0.09999996,  1.        ]),
 [[0.0, 0.5, -0.1, -0.2, 0.5],
  [0.5, 1.25, -0.05, -0.1, 0.25],
  [-0.1, -0.05, 0.51, 0.02, -0.05],
  [-0.2, -0.1, 0.02, 0.54, -0.1],
  [0.5, 0.25, -0.05, -0.1, 1.25]])

Also the SDP cone is a symmetric cone!

Are there more cones?

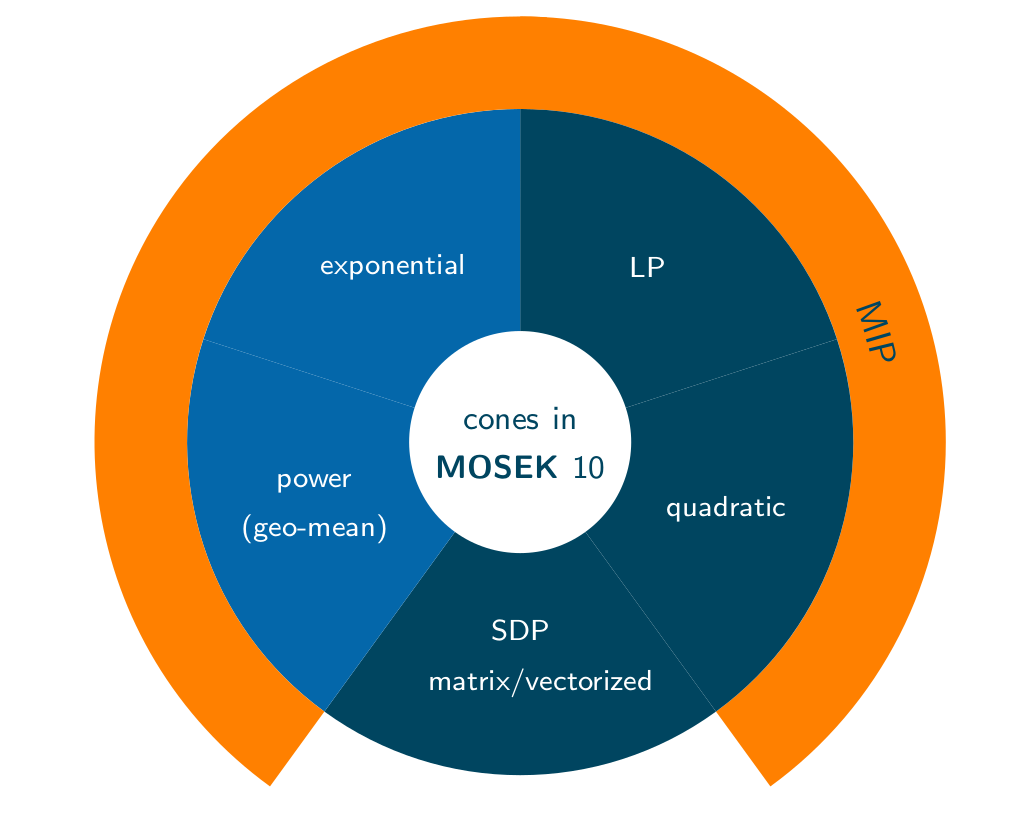
"Exotic" cones:

• For every convex function $g(x)$ the set $$\mathcal{K}: = \text{cl}\{(y,s,x)~|~ y\geq s\cdot g(x/s)\}$$ is a closed pointed convex cone. So $y\geq g(x) \Longleftrightarrow (y,1, x)\in \mathcal{K}.$

• Several prominent matrix cones (copositive, completely positive, doubly non-negative, ...)

But for every new cone, questions arise:

• How de we handle it computationally? Barrier function?
• Is it tractable?

Do we need more cones?

Remember the folklore: "Almost all convex constraints that arise in practice are representable using these 5 cones."

• But: for example, for the logarithmic mean temperature difference $$t\geq\left(\frac{\log(x/y)}{x-y}\right)^\beta,$$ no reformulation using linear, quadratic, exp, power and SDP cones is known.

• Also, a new cone may lead to less reformulation. Examples:
  • $t\geq |x|^{3/2}$ through quadratic or power cone?
  • Geometric mean through power or geo-mean cone?

Further remarks

• MOSEK Fusion is routed through the optimizer API
  • more low-level
  • works with matrix-oriented affine expressions and conic domains

• MOSEK 10 introduced disjunctive constraints: $$[A^1x\leq b_1]\vee\ldots\vee[A^kx\leq b_k]$$ E.g. indicator or complementarity constraints, semi-continuous variables, SOS1,...

# x_i = 2.5 for any one of i = 0,1,2,3
m.disjunction([DJC.term(x.index(i), Domain.equalsTo(2.5)) for i in range(4)])

• Both Fusion and the optimizer API support Conic Duality.

dualsolvals = x.dual()

Further reading

• A. Ben-Tal & A. Nemirovski: Lectures on Modern Convex Optimization, SIAM (2001).

• ### $\texttt{www.mosek.com}\longrightarrow$ Documentation

  • Manuals
  • The MOSEK Modeling Cookbook
  • The Conic Modeling Cheatsheet
  • Notebook collection

• Google CoLab notebook with examples of this talk: https://colab.research.google.com/drive/1j2TxnNemD5Wb5Au8gqKXLqaMqHrKtX0n?usp=sharing

Questions?